Zlomky
1) Vypočítejte příklady na sčítání a odčítání zlomků. Výsledky uvádějte v základním tvaru:
3 5 + 2 3 =
7 10 + 4 5 =
3 2 + 7 6 =
1 8 + 1 11 =
6 7 + 1 21 =
1 5 + 5 8 =
5 4 - 1 3 =
3 4 - 4 11 =
8 3 - 5 9 =
15 7 - 4 3 =
7 2 - 1 3 =
12 5 - 3 12 =
2) Vypočítejte příklady na násobení a dělení zlomků. Výsledky uvádějte v základním tvaru:
10 3 · 6 5 =
1 20 · 4 1 =
4 5 · 15 8 =
5 12 · 3 15 =
8 9 · 18 2 =
4 12 : 4 3 =
1 18 : 1 9 =
11 8 : 22 3 =
9 5 : 3 20 =
18 7 : 27 21 =
3) Vytvořte základní tvar z těchto zlomků:
3 12 =
15 12 =
30 45 =
3 21 =
18 20 =
27 9 =
15 18 =
22 16 =
24 26 =
5 25 =
4) Převeďte smíšená čísla na nepravé zlomky:
3 3 11 =
1 4 5 =
7 1 7 =
8 5 12 =
10 2 7 =
6 3 13 =
5 5 6 =
12 1 8 =
9 5 7 =
11 11 12 =
5) Převeďte nepravé zlomky na smíšená čísla:
31 3 =
42 4 =
32 5 =
47 9 =
111 7 =
71 6 =
109 11 =
55 4 =
67 15 =
87 10 =
6) Vypočítejte příklady se smíšenými čísly. Výsledky uvádějte v nepravém zlomku v základním tvaru:
3 1 3 + 3 2 3 =
2 1 5 + 3 1 7 =
4 1 10 + 5 1 3 =
7 4 5 + 1 2 3 =
8 3 10 + 12 1 5 =
7 12 13 - 2 6 13 =
9 1 5 - 7 3 7 =
3 19 20 - 1 4 5 =
7 8 9 - 3 4 5 =
11 1 11 - 10 1 10 =
7) Porovnejte dva zlomky pomocí <, >, =
3 10 a 4 20
3 5 a 4 7
5 8 a 3 4
7 12 a 5 9
2 3 a 3 5
5 6 a 7 10
4 9 a 1 2
11 15 a 7 10
5 6 a 15 18
9 8 a 7 5
8) Vypočítejte složené zlomky. Výsledky uvádějte v základním tvaru:
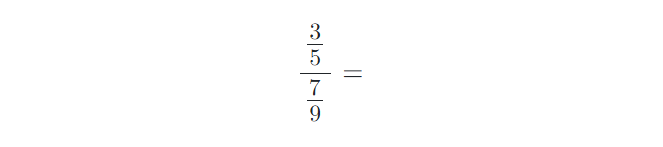
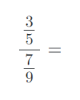
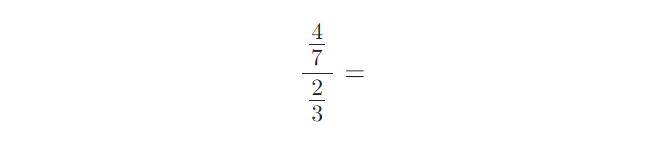
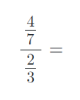
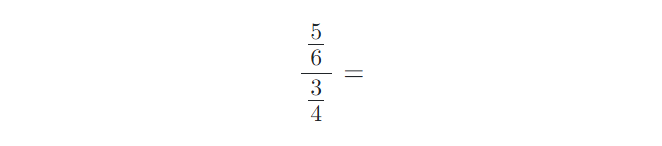
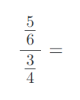
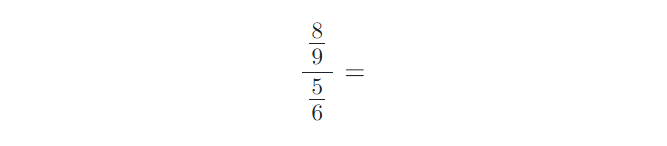
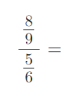
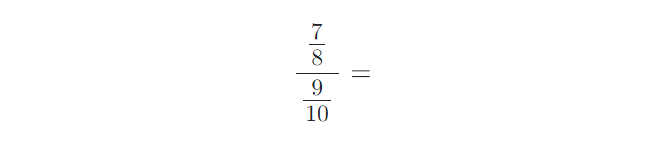
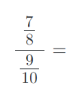
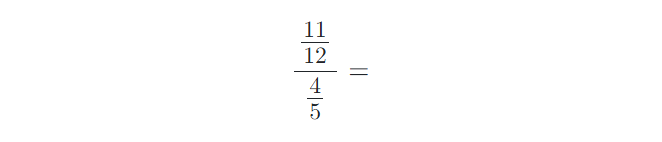
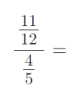
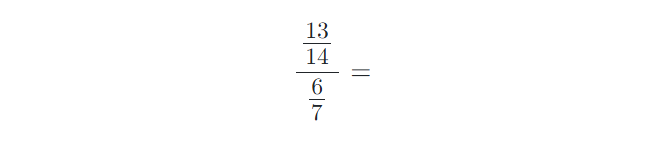
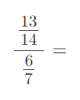
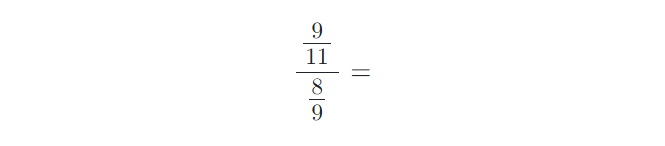
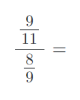
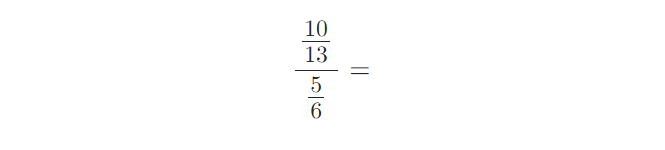
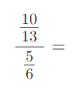
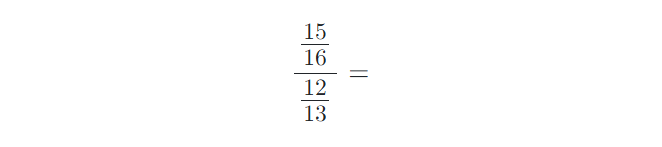
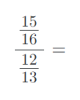
9) Vypočítejte příklady na zlomky. Výsledky uvádějte v základním tvaru:
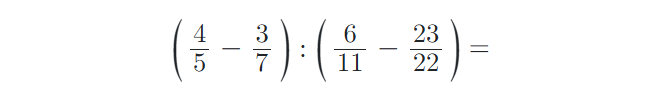
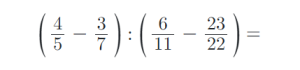
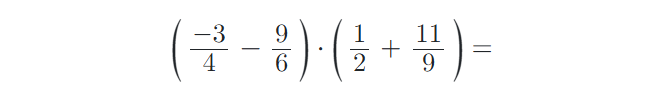
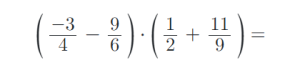
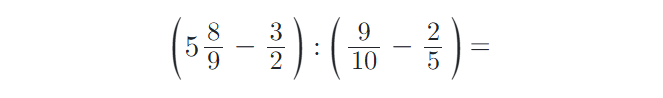
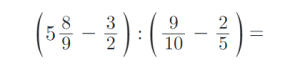
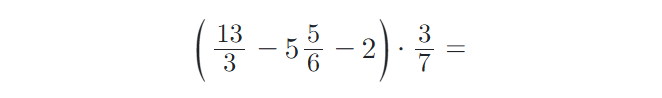
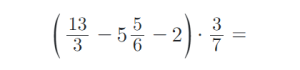
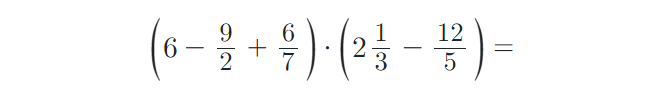
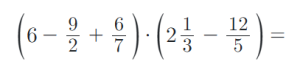
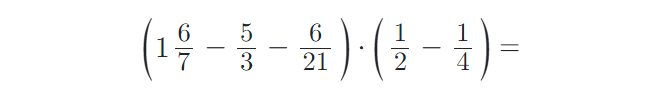
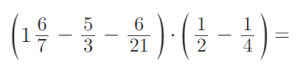
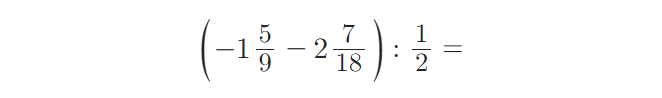
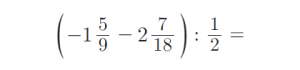
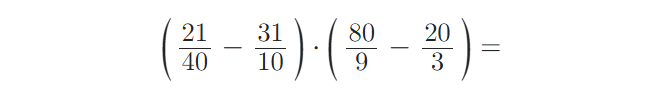
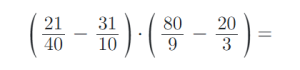
Přečtěte si o tématu dále

Témata k přijímacím zkouškám z matematiky
Přehled nejčastějších typů úloh: počítání se zlomky a vzorci, rovnice, slovní úlohy, geometrie i procenta. Upozorníme na časté chyby a dáme ti tipy, jak se jim vyhnout. Asi první blok, co člověka napadne je klasické počítání ať už například s mocninami, odmocninami nebo velmi často zlomky. V těchto typech příkladů si student sbírá první body, protože tyto úlohy se řadí mezi ty lehčí. Je však důležité, aby uchazeč neudělal zbytečné chyby jako třeba to, že by celý příklad vynásobil společným jmenovatelem (to se dělá totiž až následně u rovnic), dále uvedení výsledku s opačným znamínkem nebo neuvedení výsledného zlomku v základním tvaru, protože i to je bohužel bráno za chybu a pokud je příklad za 2 body, jeden se automaticky strhává.

Jak správně krátit zlomky
Krácení zlomků je základní dovednost, která vám usnadní celý svět matematiky.
Vyzkoušejte si to podle jednoduchých kroků a už nikdy se v tom neztratíte!
Co znamená krátit zlomek?
Krácení znamená zmenšení čitatele i jmenovatele zlomku stejným číslem. Výsledný zlomek je jednodušší, ale stále má stejnou hodnotu jako ten původní. Krácení zlomků většinou používáme při násobení zlomků nebo pro získání zlomku v základním tvaru.

Jak převádět smíšená čísla na zlomky
Převádění smíšených čísel na zlomky je jednoduchá, ale důležitá dovednost. Pomůže vám lépe počítat se zlomky a pracovat se všemi čísly stejně. Co je to smíšené číslo? Smíšené číslo je kombinace celého čísla a zlomku. Například číslo 3 a 1/2 zapisujeme jako 3½. Používáme ho, když máme celek nebo celky a ještě nějakou část navíc jako třeba 3 celé pizzy a půlku další.

Jak sčítat a odčítat zlomky s různými jmenovateli
Sčítání a odčítání zlomků může být na první pohled trochu zákeřné a hlavně když mají různé jmenovatele.
Ale jakmile se naučíte jednotný postup, zvládnete každý příklad levou zadní.
Proč je potřeba mít stejné jmenovatele?
Abychom mohli zlomky sčítat nebo odčítat, musí mít stejného „společného jmenovatele“, což je tedy spodní číslo ve zlomku. Bez toho to nepůjde a nebude fungovat, protože jinak sčítáme jablka a hrušky.
Jak najít společného jmenovatele?
Nejlépe funguje tzv. nejmenší společný násobek obou jmenovatelů.
