Obrazce
1) Vypočítejte úlohy na obvod a obsah rovinných obrazců:
Určete obvod a obsah obdélníku, jehož strany jsou 5 cm a 8 cm.
Obdélník má obvod 50 cm a jedna z jeho stran měří 15 cm. Vypočítejte délku druhé strany a obsah obdélníku.
Obvod půlkruhu je 30 cm. Vypočítejte obsah půlkruhu.
Kosodelník má obvod 36 cm a délku jedné strany 10 cm. Vypočítejte délku druhé strany a obsah kosodelníku, pokud je výška kolmá na zadanou stranu kosodelníku 6 cm.
2) Vypočítejte na základě vlastností rovinných obrazců:
V kosočtverci je α = 70°. Jak velký je úhel β?
Máte rovnoběžník ABCD. Strany AB a CD jsou rovnoběžné, stejně jako strany AD a BC. Pokud je délka strany |AB|= 8 cm a |AD|= 6 cm, zjistěte, jaká je délka stran CD a BC.
V rovnoběžníku ABCD je úhel |∢DAB|= 40°. Určete velikost všech ostatních úhlů rovnoběžníku.
|∢CDA|= 140°
V rovnoběžníku ABCD jsou AC a BD úhlopříčky. Úhly, které tyto úhlopříčky svírají, jsou rovny 60°. Určete, zda je rovnoběžník kosočtverec.
3) Vypočítejte slovní úlohy na rovinné obrazce:
Kolik dlaždic o rozměrech 25 cm × 25 cm bude potřeba na pokrytí čtvercového dvora o straně 5 m?
Kruh má průměr 25 m. Čtverec má délku strany 15 m. Kolikrát je větší délka kružnice než obvod čtverce?
V parku se nachází pavilon ve tvaru obdélníku o délce 30 m a šířce 10 m. Vedle pavilonu je střešní terasa ve tvaru kosočtverce, jehož diagonály měří 18 m a 24 m. Jaký je rozdíl v ploše mezi pavilonem a terasou?
Na závodní dráze je tvar okruhu, který má průměr 50 m. Vedle dráhy se nachází pozemek ve tvaru rovnoramenného lichoběžníku se základnami 12 m a 20 m a výškou 5 m. Jaký je rozdíl ploch mezi okruhem a pozemkem?
První zahrada má tvar obdélníku o délce 20 m a šířce 15 m. Druhá zahrada je tvaru rovnoramenného lichoběžníku se základnami 5 m a 15 m a výškou 4 m. Jaká je rozdíl ploch obou zahrad?
Lichoběžník má základny 10 m a 18 m, výšku 6 m. Kosočtverec má diagonály 12 m a 16 m. Půlkruh má poloměr 8 m. Kolikrát je plocha lichoběžníku menší než plocha kosočtverce? Kolikrát je plocha kosočtverce menší než plocha půlkruhu?
4) Narýsujte:
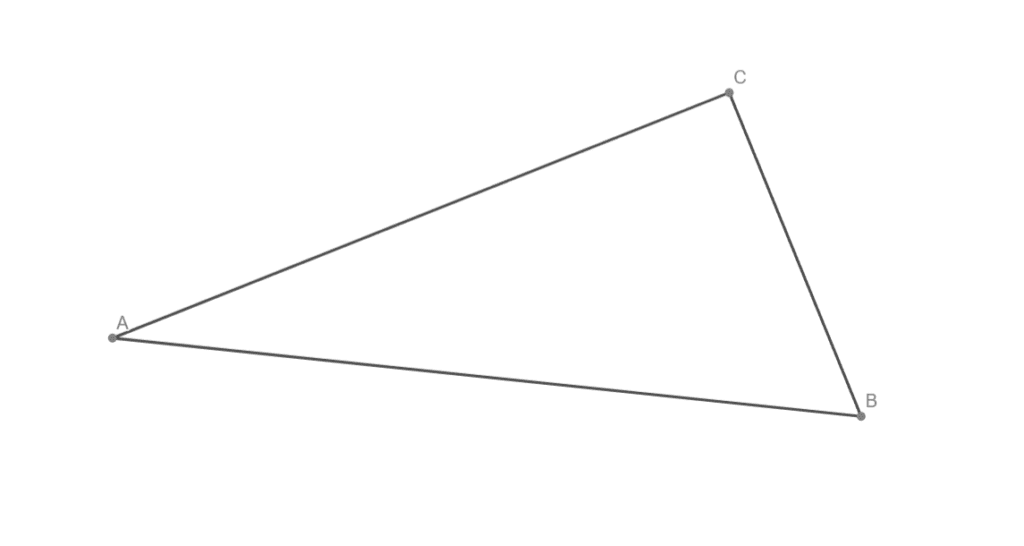
Všechny těžnice v daném trojúhelníku
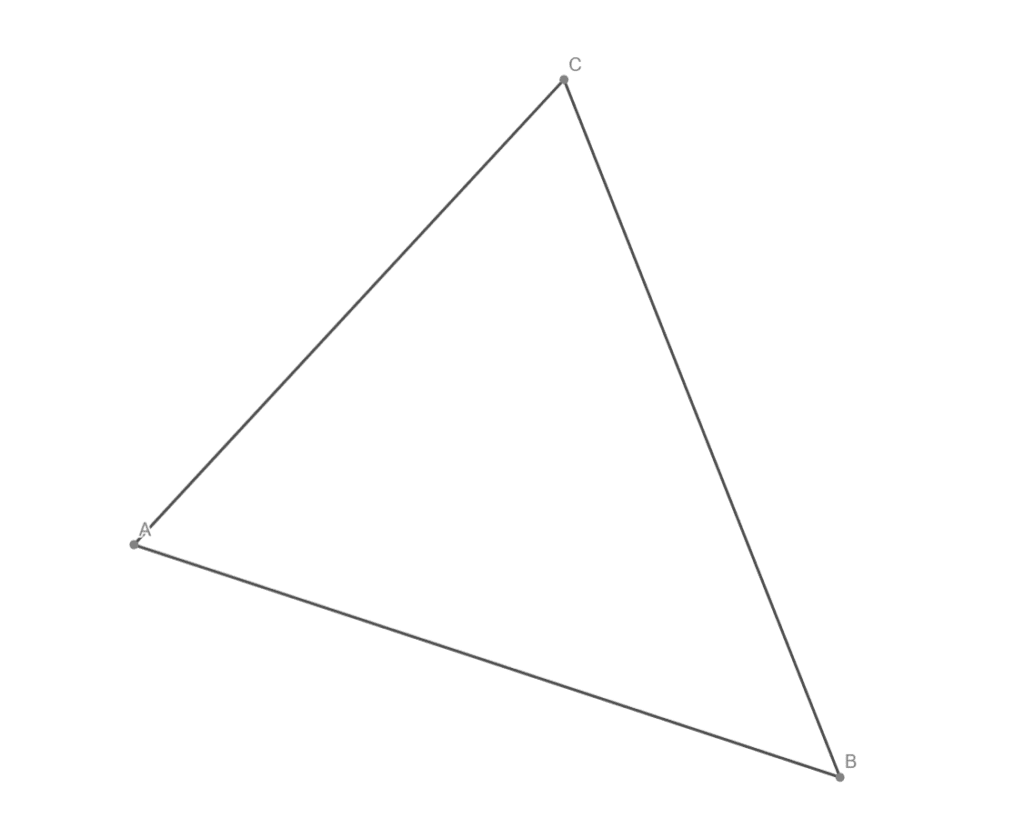

Všechny těžnice v daném trojúhelníku a vyznačte těžiště
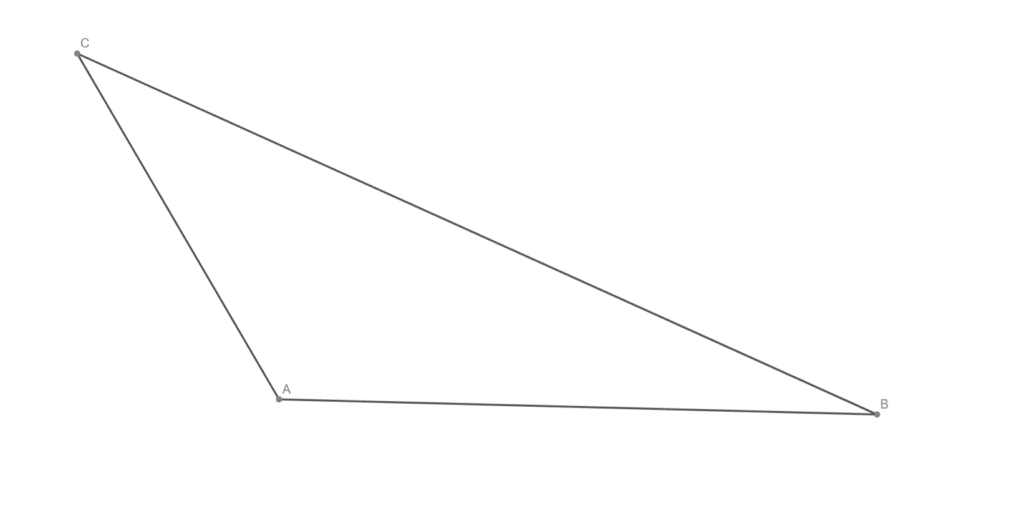
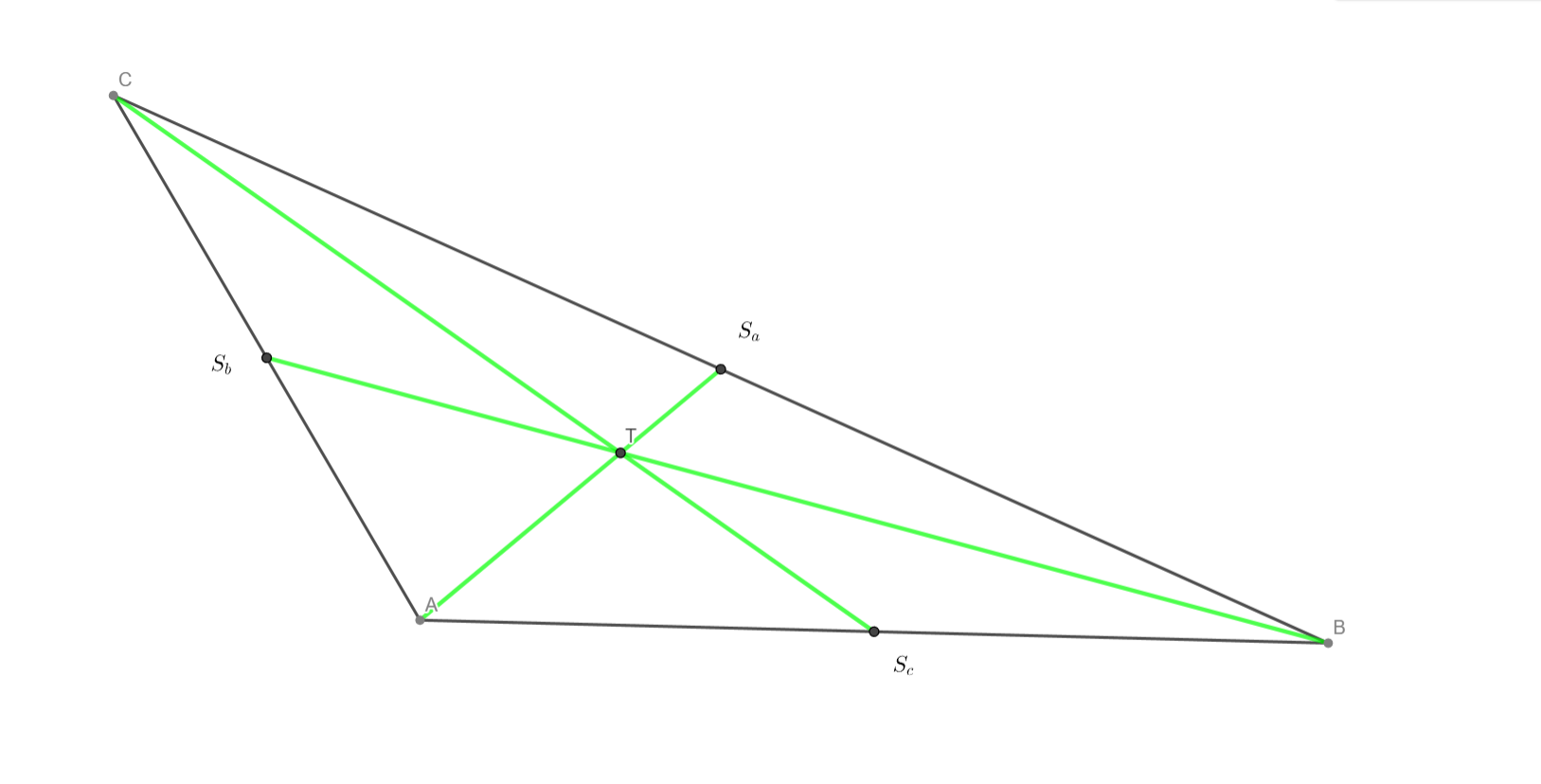
Všechny výšky v daném trojúhelníku
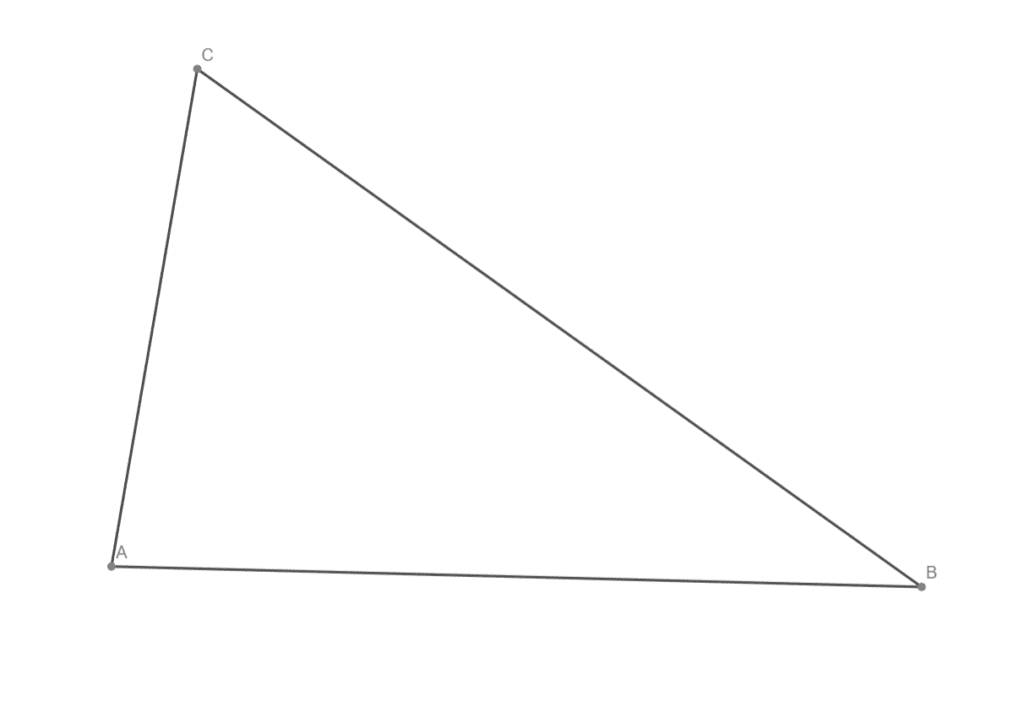

Všechny výšky v daném trojúhelníku a vyznačte ortocentrum
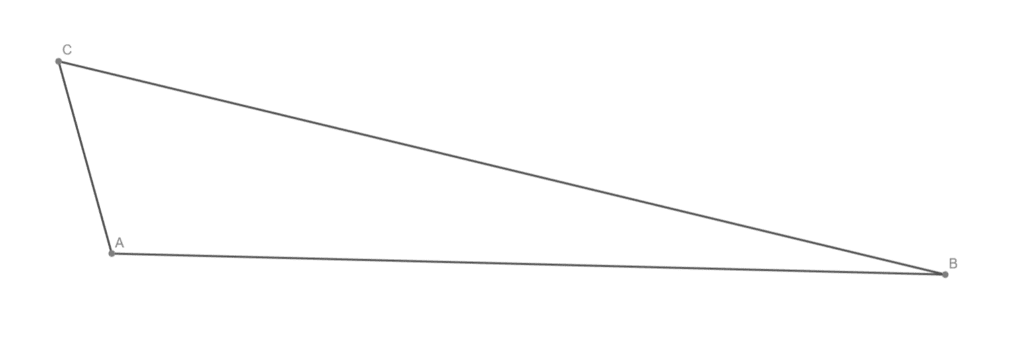
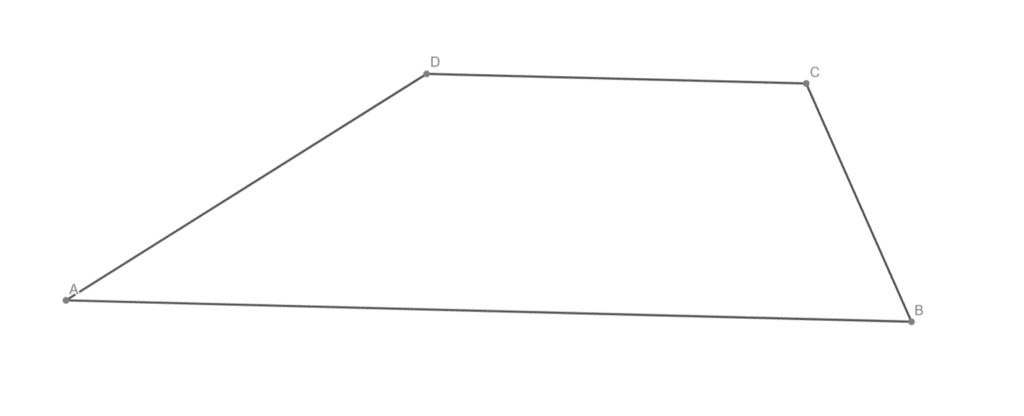
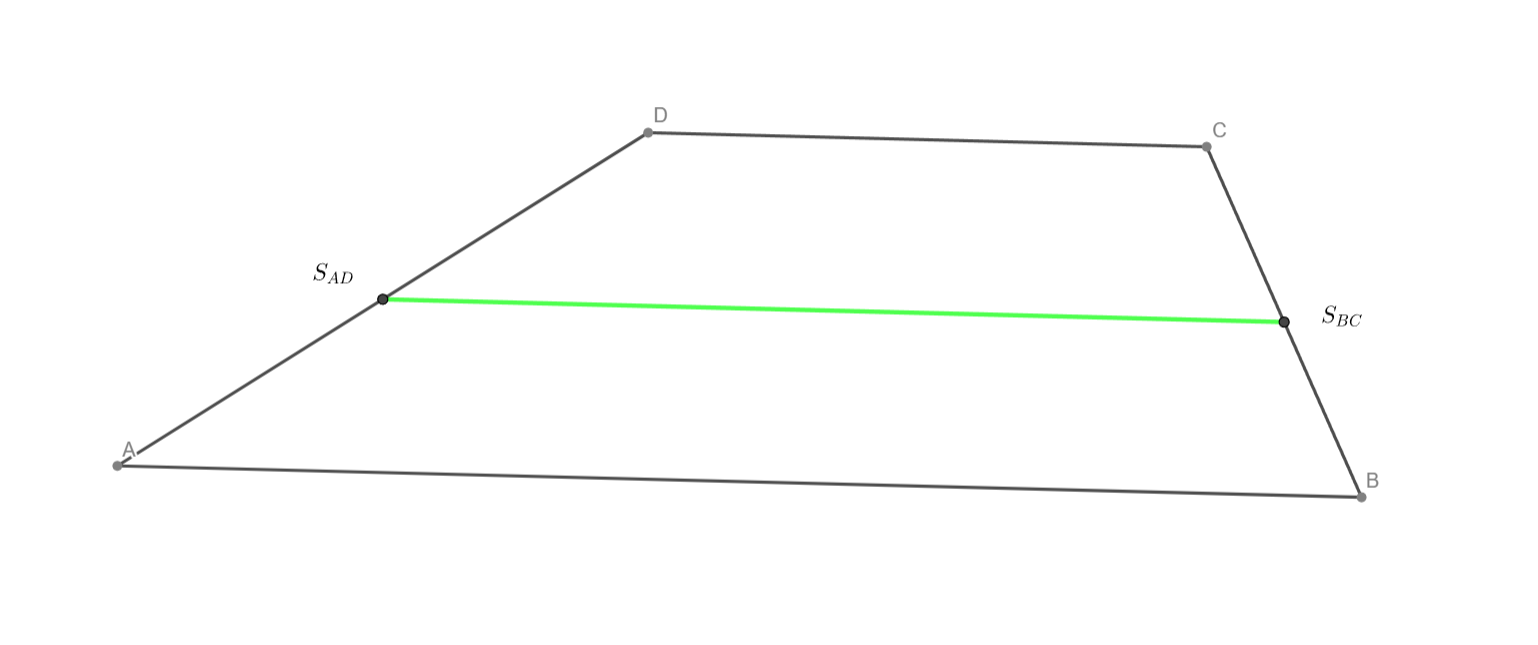
Střední příčku v daném lichoběžníku
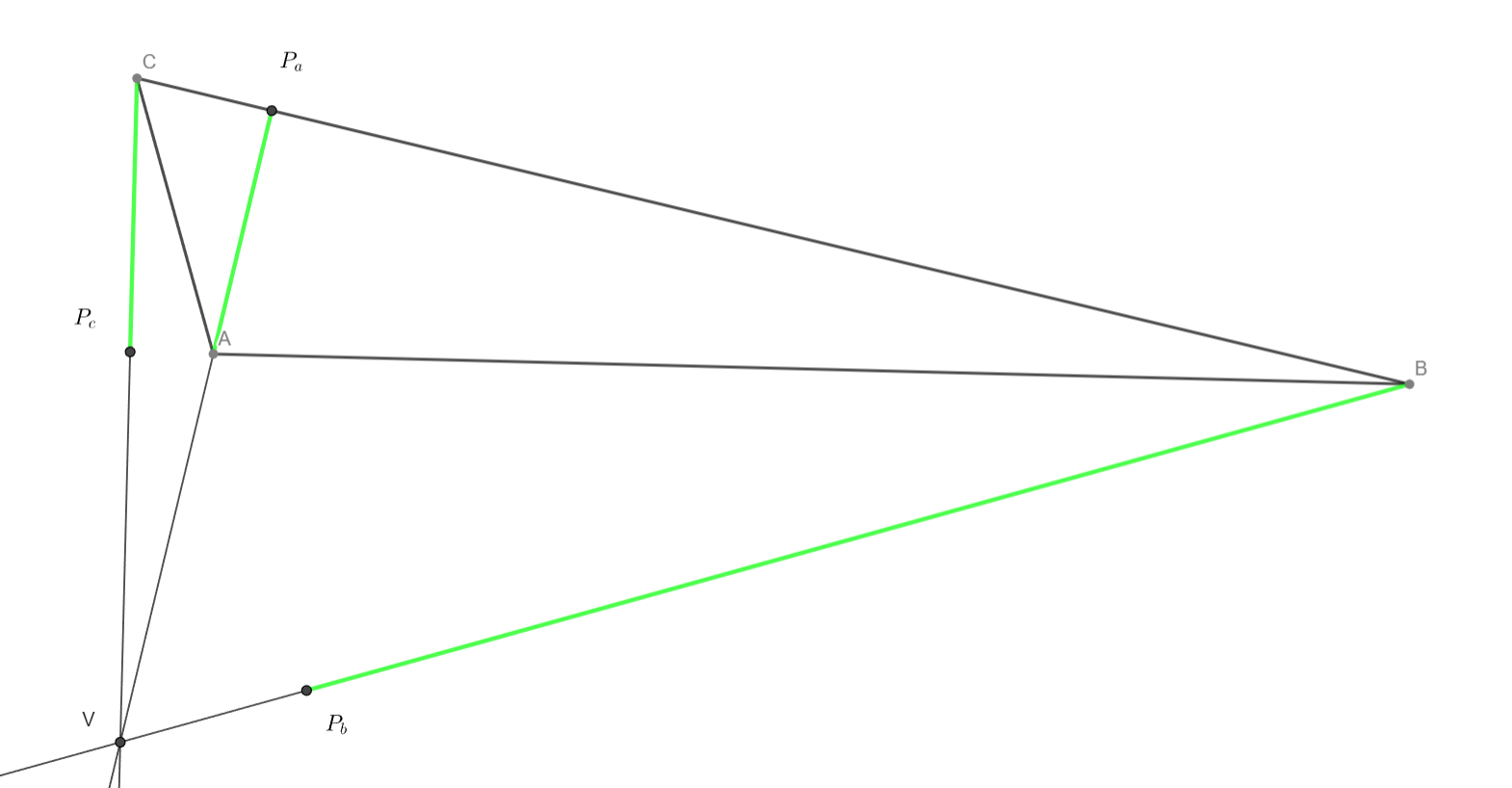
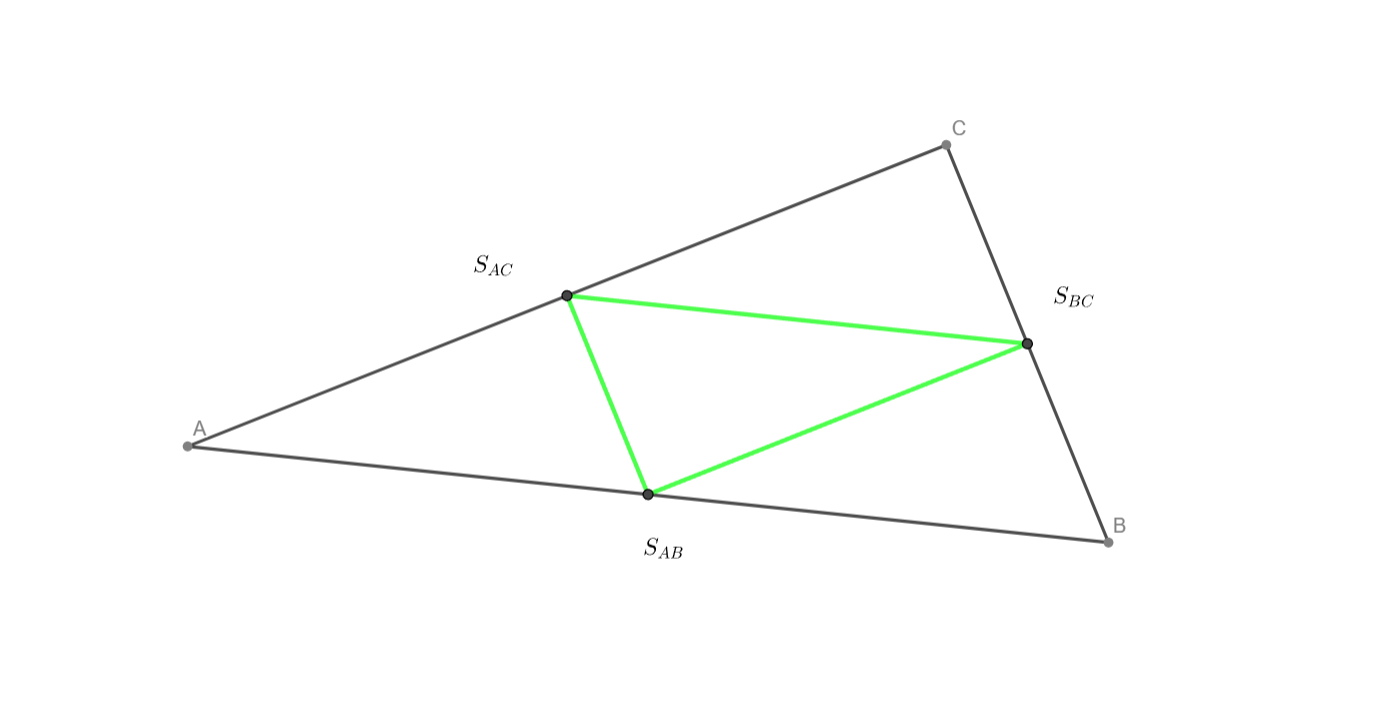
Střední příčky v daném trojúhelníku
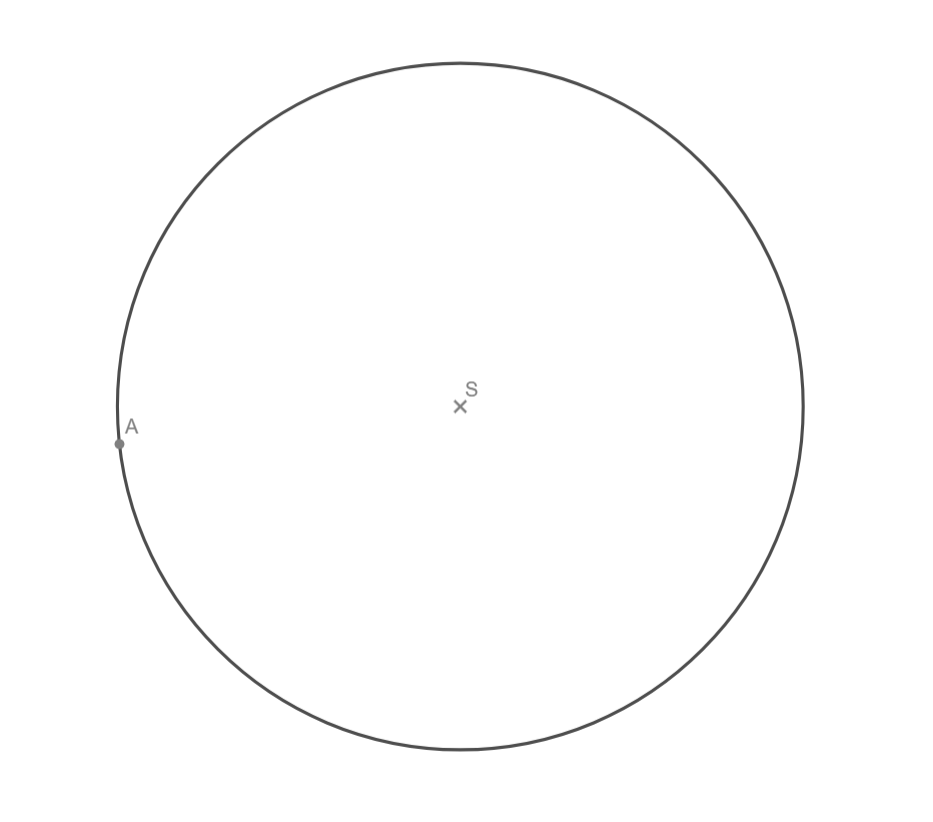
Všechny tětivy dlouhé 5,5 cm, které budou mít počátek v bodě A na kružnici o poloměru 5 cm

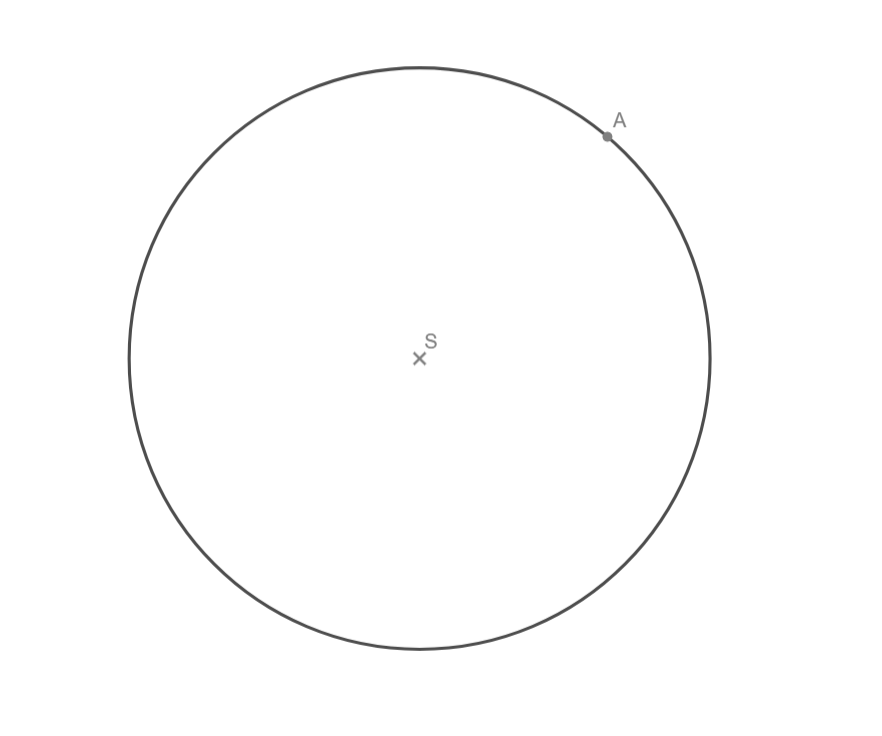
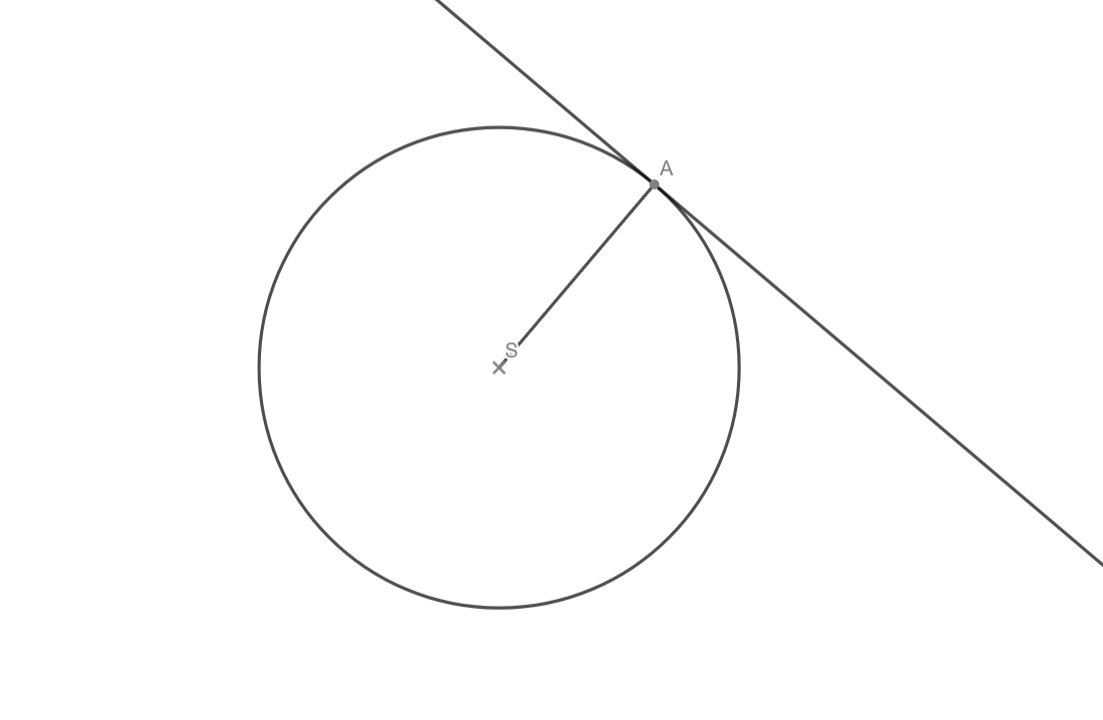
Tečnu procházející bodem A
Přečtěte si o tématu dále

Jak poznat základní rovinné útvary
Základní rovinné obrazce se učíme už na prvním stupni, ale opakování se hodí i na vyšších úrovních matematiky. Pokud je dokážeme rychle rozeznat podle jejich vlastností, ulehčí nám to nejen geometrii, ale i úlohy z praxe. Proč se učíme rovinné obrazce? Znalost základních geometrických tvarů není jen školní látkou. Využijeme ji i v běžném životě například při plánování stavby, při práci s mapou nebo třeba při určování velikosti plochy v bytě. Čím lépe dokážeme obrazce rozeznat a popsat jejich vlastnosti, tím snazší pro nás bude navazující učivo i praktické využití matematiky.
Jak vypočítat obvod a obsah obrazce
Teď když poznáme základní rovinné obrazce, budeme s nimi počítat, konkrétně se bude jednat o obvod a obsah rovinných útvarů. Co je obvod a obsah? Každý rovinný obrazec má dvě základní „velikosti“: obvod – délka čáry, která obrazec ohraničuje, obsah – plocha uvnitř obrazce. Tyto dva pojmy spolu souvisejí, ale nejsou totéž. Obvod měří délku okraje, obsah měří, kolik místa obrazec zabírá.

Jak narýsovat pravidelné obrazce
Teď víme, jak cca budou vypadat základní rovinné obrazce. Ale co když se bude jednat o pravidelné rovinné obrazce? Co se změní? Co jsou pravidelné útvary? Pravidelný obrazec znamená, že má všechny strany stejně dlouhé a všechny úhly stejně velké. Typickými příklady jsou čtverec, rovnostranný trojúhelník, pravidelný pětiúhelník, šestiúhelník nebo osmiúhelník.

Jak převádět jednotky obsahu
U počítání obsahu obrazců nám vychází jednotky čtvereční (jednotky na druhou). Proto je potřeba vědět, jak s nimi pracovat, abychom neudělali chybu v převodu těchto jednotek. Co jsou jednotky obsahu? Jednotky obsahu používáme k vyjádření velikosti plochy. Nejčastěji se setkáváme se čtverečními jednotkami, jako je cm², m² nebo km². Každá z těchto jednotek vyjadřuje, jak velká část roviny je pokryta čtvercem o dané délce strany. Například 1 m² odpovídá ploše čtverce se stranou 1 metru.
