Konstrukční úlohy
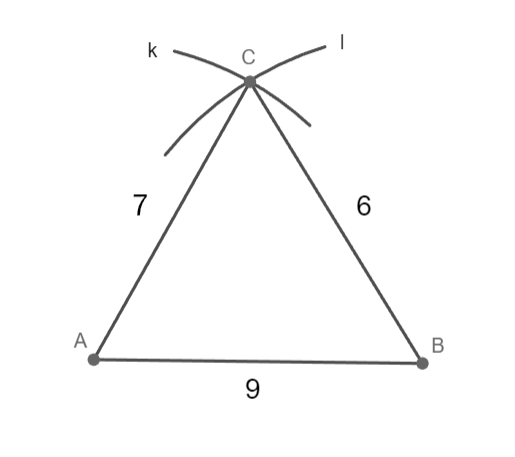
a = 6 cm; b = 7 cm; c = 9 cm
Sestrojte trojúhelník ABC.
AB
C
_________________
C ∈ k; k(A; 7 cm)
C ∈ l; l(B; 6 cm)
C ∈ k ∩ l
1) AB; |AB|= 9 cm
2) k; k(A; 7 cm)
3) l; l(B; 6 cm)
4) C; C ∈ k ∩ l
5) trojúhelník ABC
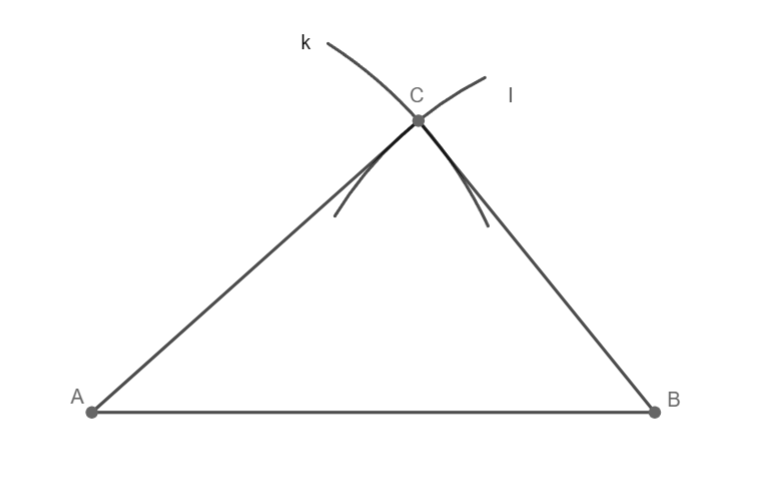
Trojúhelník ABC souhlasí, 1 řešení.
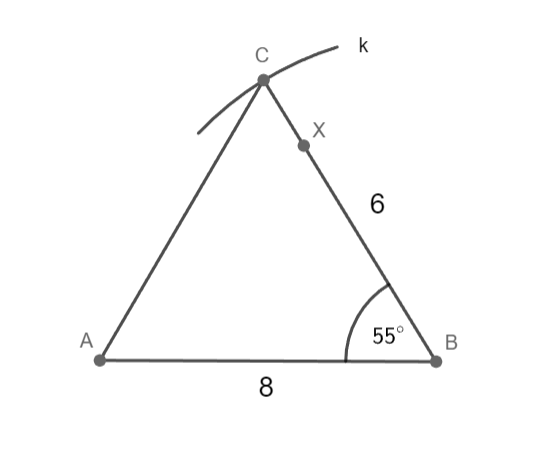
a = 6 cm; c = 8 cm; β = 55°
Sestrojte trojúhelník ABC.
AB
C
_________________
C ∈ k; k(B; 6 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
1) AB; |AB|= 8 cm
2) k; k(B; 6 cm)
3) ∢ABX; |∢ABX|= 55°
4) C; C ∈ k ∩ ⟼ BX
5) trojúhelník ABC
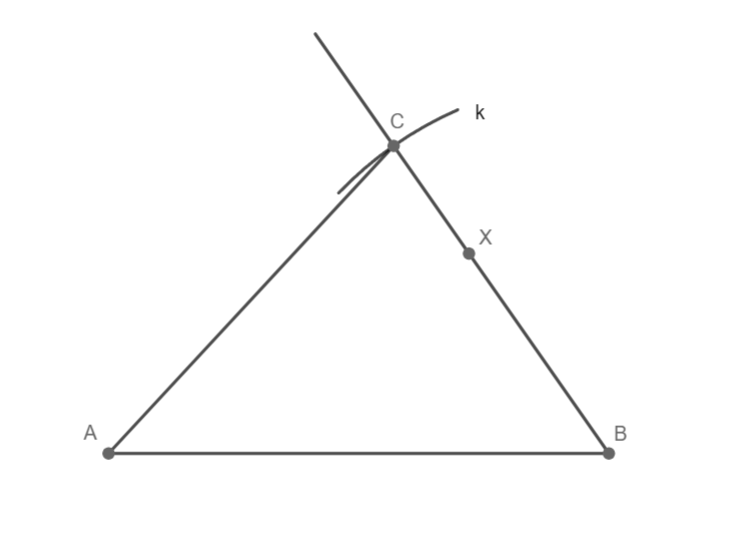
Trojúhelník ABC souhlasí, 1 řešení.
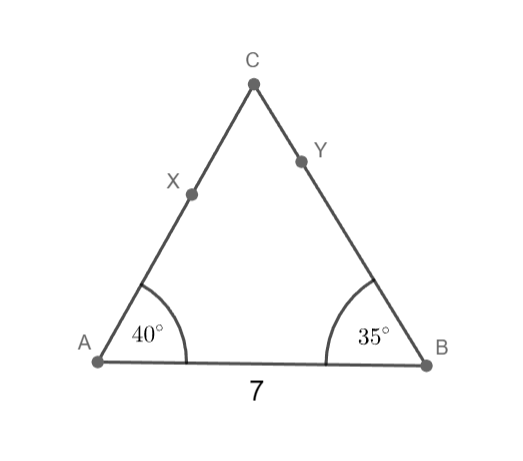
c = 7 cm; α = 40°; β = 35°
Sestrojte trojúhelník ABC.
AB
C
________________
C ∈ ⟼ AX
C ∈ ⟼ BY
C ∈ ⟼ AX ∩ ∈ ⟼ BY
1) AB; |AB|= 7 cm
2) ∢BAX; |∢BAX|= 40°
3) ∢ABY; |∢ABY|= 35°
4) C; C ∈ ⟼ AX ∩ ∈ ⟼ BY
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
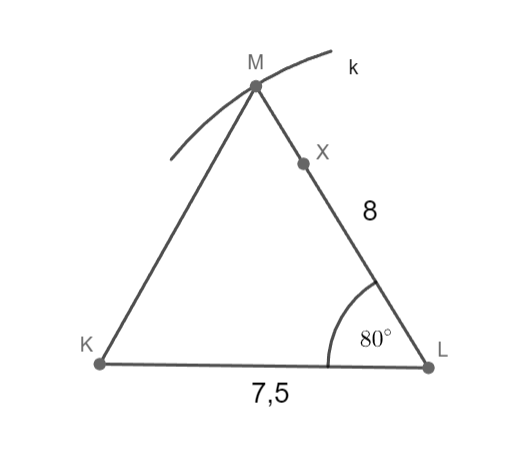
k = 8 cm; m = 7,5 cm; |∢KLM|= 80°
Sestrojte trojúhelník KLM.
KL
M
________________
M ∈ k; k(L; 8 cm)
M ∈ ⟼ LX
M ∈ k ∩ ⟼ LX
1) KL; |KL|= 7,5 cm
2) k; k(L; 8 cm)
3) ∢KLX; |∢KLX|= 80°
4) M; M ∈ k ∩ ⟼ LX
5) trojúhelník KLM
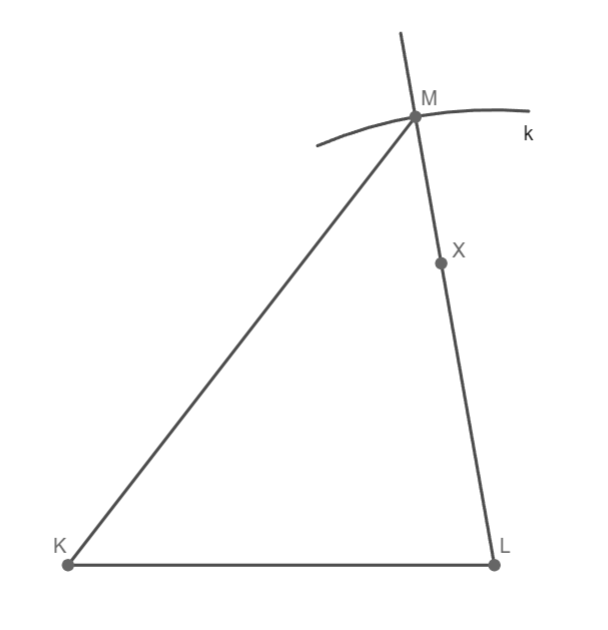
Trojúhelník KLM souhlasí, 1 řešení.
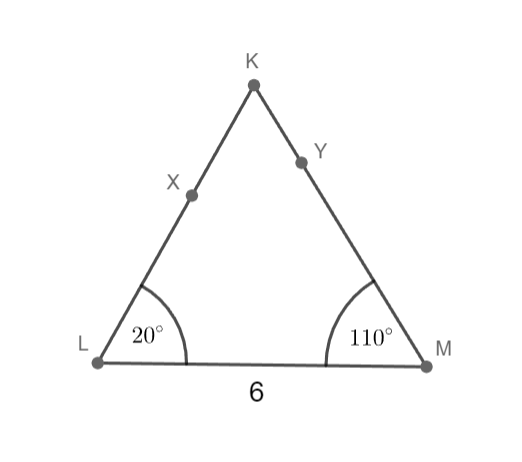
k = 6 cm; |∢KLM|= 20°; |∢LMK|= 110°
Sestrojte trojúhelník KLM.
LM
K
________________
K ∈ ⟼ LX
K ∈ ⟼ MY
K ∈ ⟼ LX ∩ ∈ ⟼ MY
1) LM; |LM|= 6 cm
2) ∢MLX; |∢MLX|= 20°
3) ∢LMY; |∢LMY|= 110°
4) K; K ∈ ⟼ LX ∩ ∈ ⟼ MY
5) trojúhelník KLM
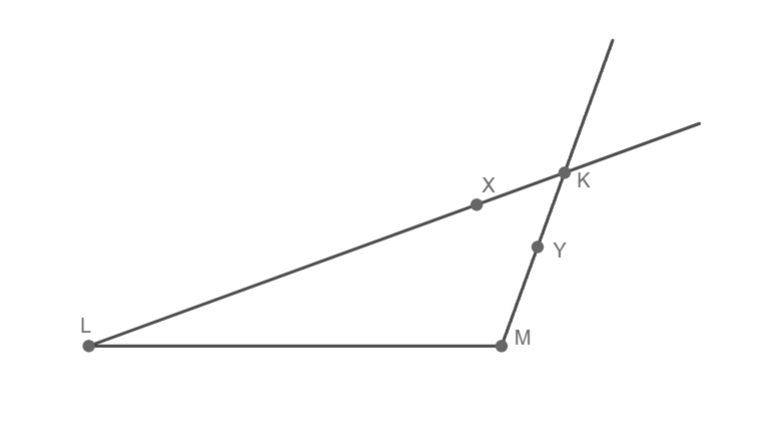
Trojúhelník KLM souhlasí, 1 řešení.
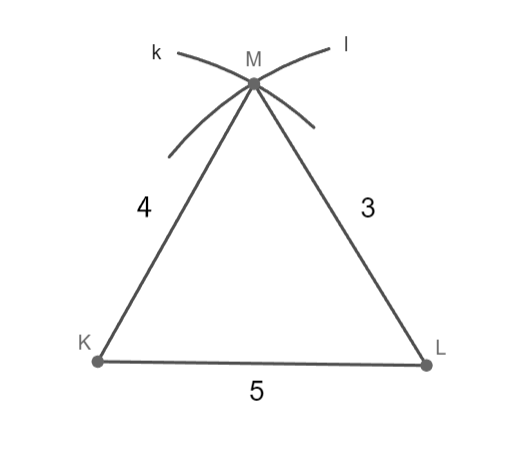
k = 3 cm; l = 4 cm; m = 5 cm
Sestrojte trojúhelník KLM.
KL
M
________________
M ∈ k; k(K; 4 cm)
M ∈ l; l(L; 3 cm)
M ∈ k ∩ l
1) KL; |KL|= 5 cm
2) k; k(K; 4 cm)
3) l; l(L; 3 cm)
4) M; M ∈ k ∩ l
5) trojúhelník KLM
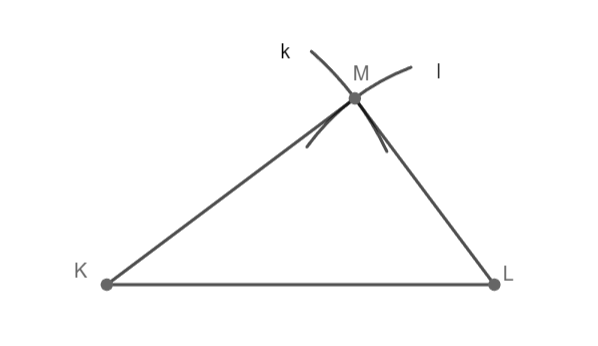
Trojúhelník KLM souhlasí, 1 řešení.
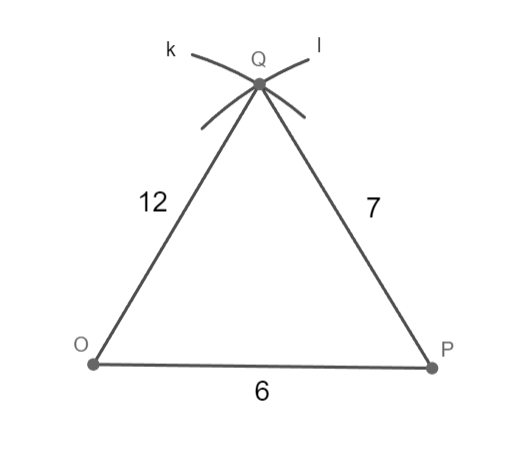
o = 7 cm; p = 12 cm; q = 6 cm
Sestrojte trojúhelník OPQ.
OP
Q
________________
Q ∈ k; k(O; 12 cm)
Q ∈ l; l(P; 7 cm)
Q ∈ k ∩ l
1) OP; |OP|= 6 cm
2) k; k(O; 12 cm)
3) l; l(P; 7 cm)
4) Q; Q ∈ k ∩ l
5) trojúhelník OPQ
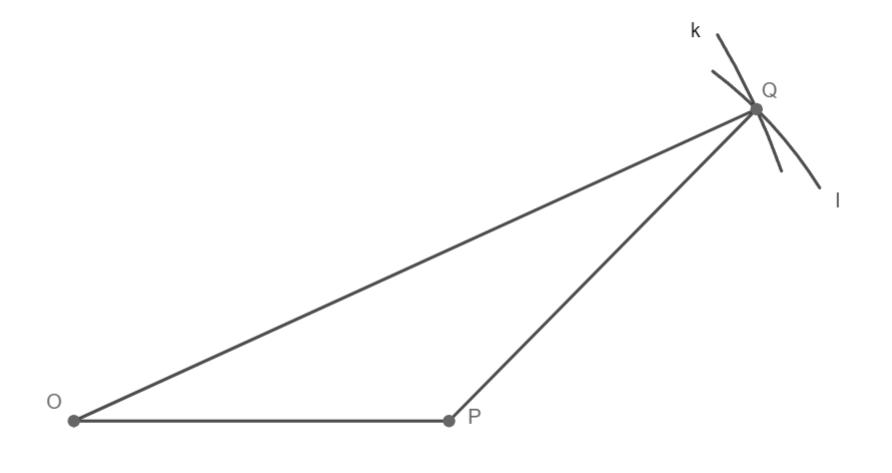
Trojúhelník OPQ souhlasí, 1 řešení.
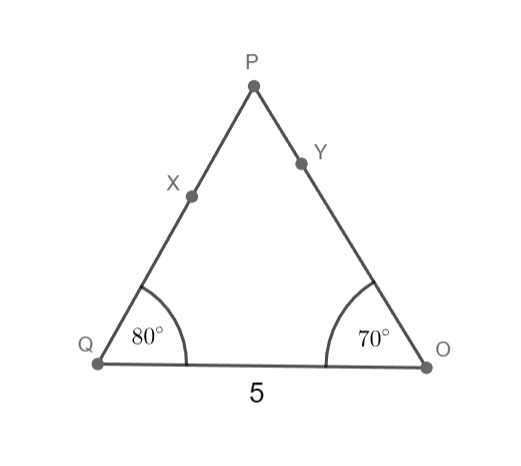
p = 5 cm; |∢QOP|= 70°; |∢PQO|= 80°
Sestrojte trojúhelník OPQ.
QO
P
________________
P ∈ ⟼ QX
P ∈ ⟼ OY
P ∈ ⟼ QX ∩ ∈ ⟼ OY
1) QO; |QO|= 5 cm
2) ∢OQX; |∢OQX|= 80°
3) ∢QOY; |∢QOY|= 70°
4) P; P ∈ ⟼ QX ∩ ∈ ⟼ OY
5) trojúhelník OPQ
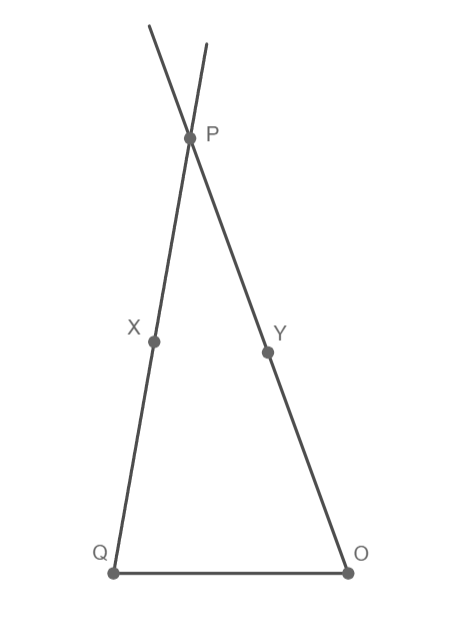
Trojúhelník OPQ souhlasí, 1 řešení.
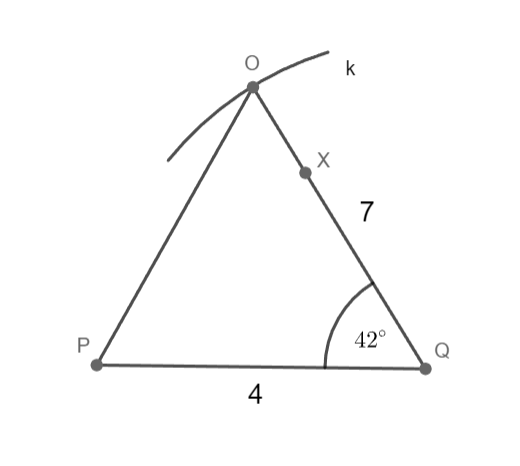
o = 4 cm; p = 7 cm; |∢PQO|= 42°
Sestrojte trojúhelník OPQ.
PQ
O
________________
O ∈ k; k(Q; 7 cm)
O ∈ ⟼ QX
O ∈ k ∩ ⟼ QX
1) PQ; |PQ|= 7,5 cm
2) k; k(Q; 7 cm)
3) ∢PQX; |∢PQX|= 42°
4) O ∈ k ∩ ⟼ QX
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
m = 6 cm; n = 3,5 cm; |∢MNO|= 30°
Sestrojte trojúhelník MNO.
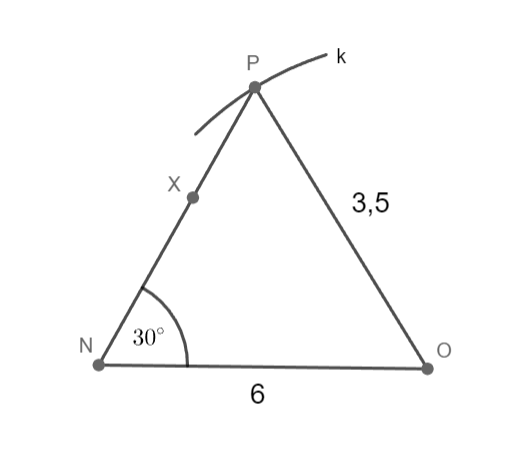
NO
M
________________
M ∈ k; k(O; 3,5 cm)
M ∈ ⟼ NX
M ∈ k ∩ ⟼ NX
1) NO; |NO|= 6 cm
2) k; k(O; 3,5 cm)
3) ∢ONX; |∢ONX|= 30°
4) M; M ∈ k ∩ ⟼ NX
5) trojúhelník MNO
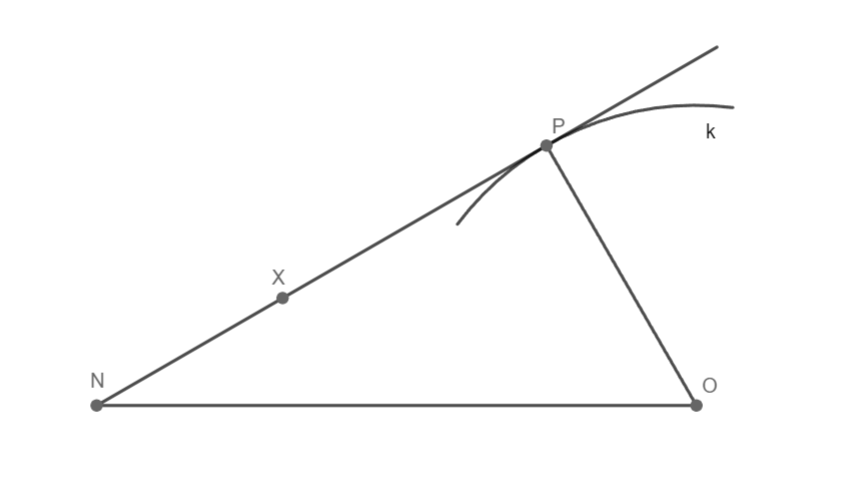
Trojúhelník MNO souhlasí, 1 řešení.
e = 6 cm; f = 4,5 cm; |∢GEF|= 90°
Sestrojte trojúhelník EFG.
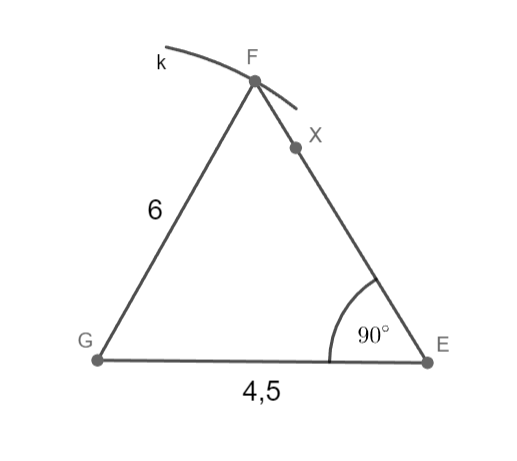
GE
F
________________
F ∈ k; k(G; 6 cm)
F ∈ ⟼ EX
F ∈ k ∩ ⟼ EX
1) EF; |EF|= 4,5 cm
2) k; k(G; 6 cm)
3) ∢GEX; |∢GEX|= 90°
4) F; F ∈ k ∩ ⟼ EX
5) trojúhelník EFG
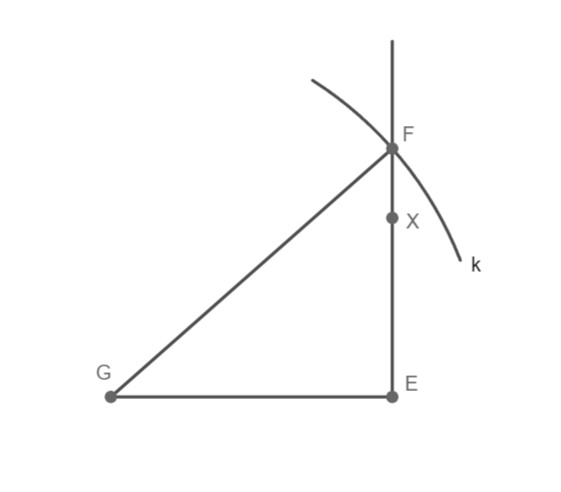
Trojúhelník EFG souhlasí, 1 řešení.
s = 10,8 cm; t = 7 cm; |∢RST|= 114°
Sestrojte trojúhelník RST.
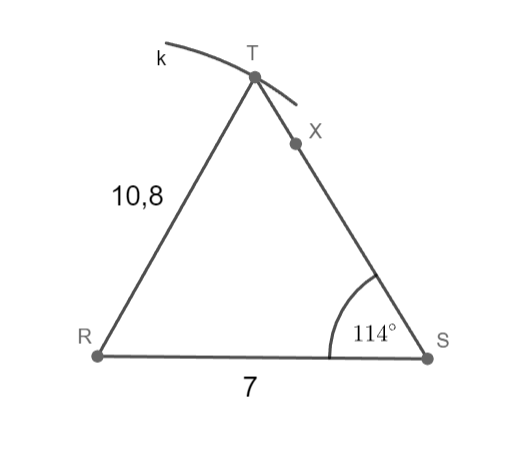
RS
T
________________
T ∈ k; k(R; 10,8 cm)
T ∈ ⟼ SX
T ∈ k ∩ ⟼ SX
1) RS; |RS|= 4,5 cm
2) k; k(R; 10,8 cm)
3) ∢RSX; |∢RSX|= 114°
4) T; T ∈ k ∩ ⟼ SX
5) trojúhelník RST
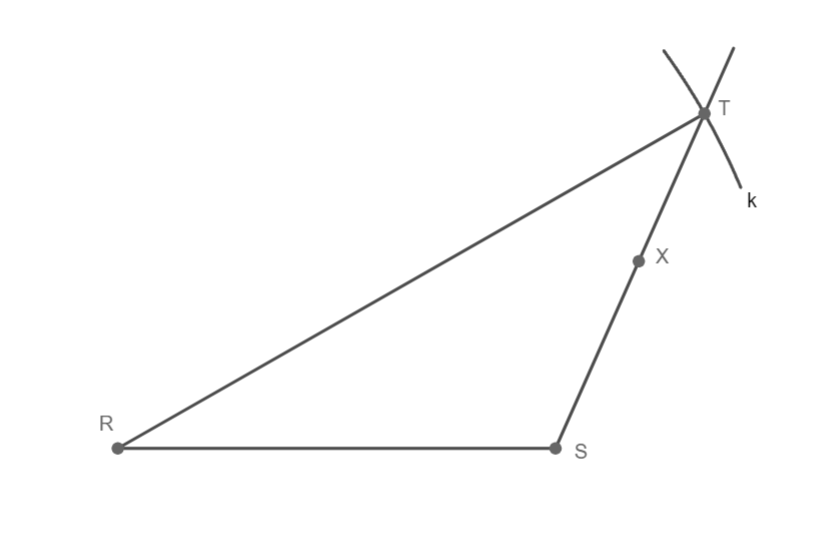
Trojúhelník RST souhlasí, 1 řešení.
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník ABCD.
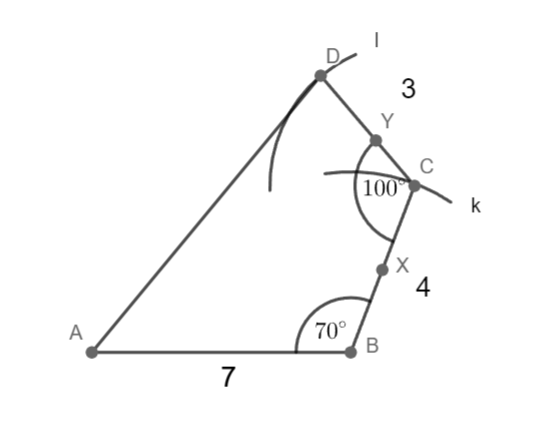
AB
CD
________________
C ∈ k; k(B; 4 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
D ∈ l; l(C; 3 cm)
D ∈ ⟼ CY
D ∈ l ∩ ⟼ CY
1) AB; |AB|= 7 cm
2) k; k(B; 4 cm)
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ k ∩ ⟼ BX
5) l; l(C; 3 cm)
6) ∢BCY; |∢BCY|= 100°
7) D; D ∈ l ∩ ⟼ CY
8) čtyřúhelník ABCD
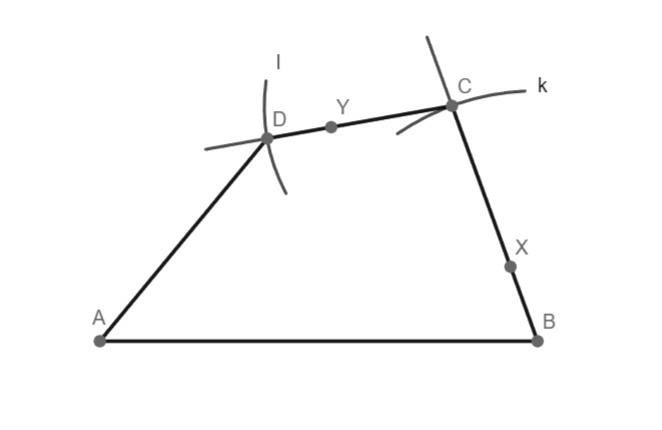
Čtyřúhelník ABCD souhlasí, 1 řešení.
a = c = 6 cm; b = d = 2,5 cm; |AC|= 7 cm
Sestrojte čtyřúhelník ABCD.
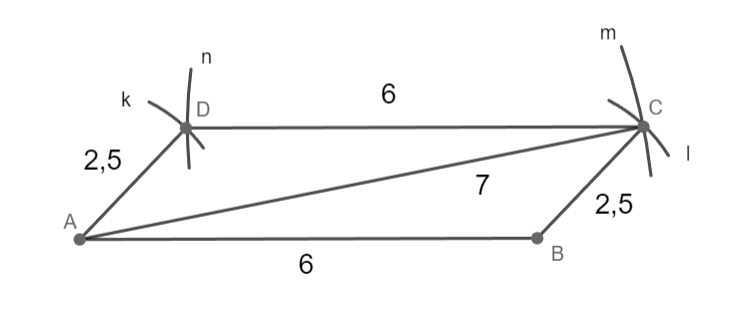
AB
CD
________________
C ∈ l; l(B; 2,5 cm)
C ∈ m; m(A; 7 cm)
C ∈ l ∩ m
D ∈ k; k(A; 2,5 cm)
D ∈ n; n(C; 6 cm)
D ∈ k ∩ n
1) AB; |AB|= 6 cm
2) l; l(B; 2,5 cm)
3) m; m(A; 7 cm)
4) C; C ∈ l ∩ m
5) k; k(A; 2,5 cm)
6) n; n(C; 6 cm)
7) D; D ∈ k ∩ n
8) čtyřúhelník ABCD
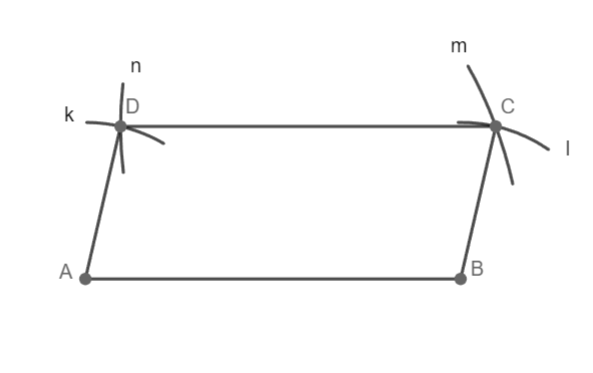
Čtyřúhelník ABCD souhlasí, 1 řešení.
d = 6,5 cm; |AC|= 7,5 cm; |BD|= 5 cm; |∢CAB|= 12°; |∢BAD|= 35°
Sestrojte čtyřúhelník ABCD.
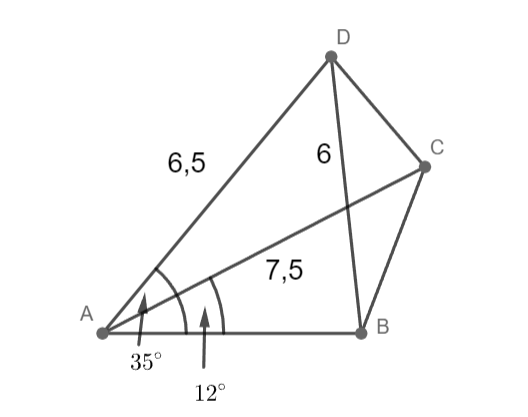
AD
CB
________________
C ∈ ⟼ AX
C ∈ k; k(A; 7,5 cm)
C ∈ ⟼ AX ∩ k
B ∈ ⟼ AY
B ∈ l; l(D; 6 cm)
B ∈ ⟼ AY ∩ l
1) AD; |AD|= 6,5 cm
2) ∢DAX; |∢DAX|= 12°
3) k; k(A; 7,5 cm)
4) C ∈ ⟼ AX ∩ k
5) ∢DAY; |∢DAY|= 35°
6) l; l(D; 6 cm)
7) B ∈ ⟼ AY ∩ l
8) čtyřúhelník ABCD
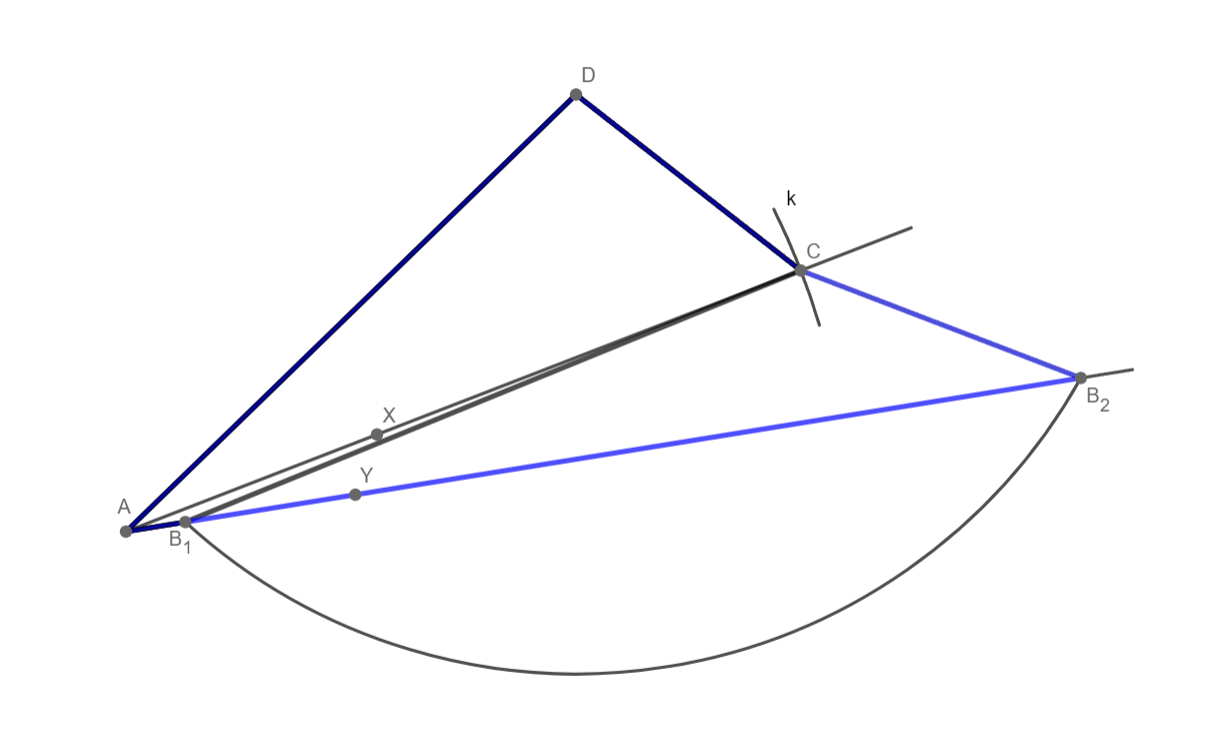
Čtyřúhelník ABCD souhlasí, 2 řešení.
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník MNOP.
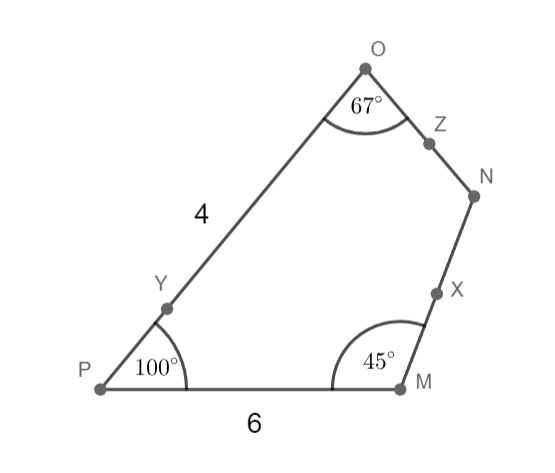
trojúhelník MPO
N
________________
N ∈ ⟼ OZ
N ∈ ⟼ MX
N ∈ ∈ ⟼ OZ ∩ ⟼ MX
1) trojúhelník MPO (SUS)
2) ∢POZ; |∢POZ|= 67°
3) ∢PMX; |∢PMX|= 45°
4) N; N ∈ ⟼ OZ ∩ ⟼ MX
5) čtyřúhelník MNOP
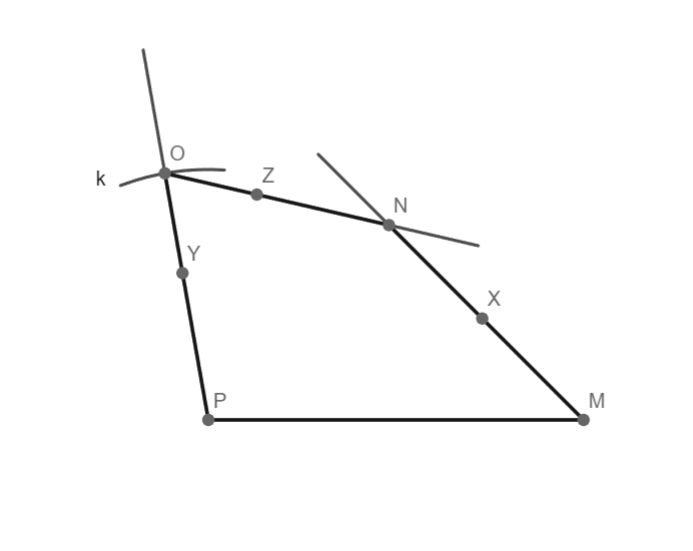
Čtyřúhelník MNOP souhlasí, 1 řešení.
|AC|=|BD|= 4 cm
Sestrojte čtyřúhelník ABCD.

AC
BD
________________
B ∈ ↔ SX; ↔ SX ⊥ AC
B ∈ k; k(S; 2 cm)
B ∈ ↔ SX ∩ k
D ∈ ↔ SX; ↔ SX ⊥ AC
D ∈ l; l(S; 2 cm)
D ∈ ↔ SX ∩ l
1) AC; |AC|= 4 cm
2) S; |SA|=|SC|, S ∈ AC
3) ↔ SX; ↔ SX ⊥ AC
4) k; k(S; 2 cm)
5) B ∈ ↔ SX ∩ k
6) l; l(S; 2 cm)
7) D ∈ ↔ SX ∩ l
8) čtverec ABCD

Čtverec ABCD souhlasí, 1 řešení.
a = 7 cm; α = 75°; β = 30°; v = 2 cm
Sestrojte lichoběžník ABCD.
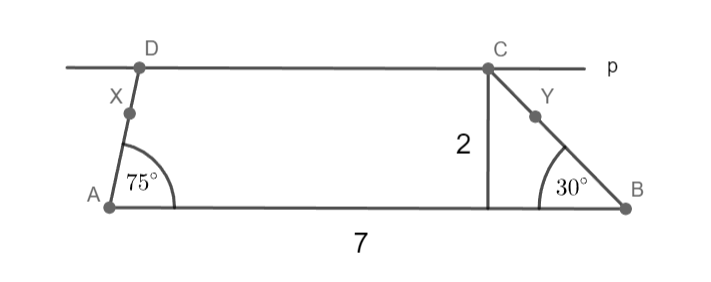
AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ AX
C ∈ p ∩ ⟼ AX
D ∈ p; p || AB
D ∈ ⟼ BY
D ∈ p ∩ ⟼ BY
1) AB; |AB|= 7 cm
2) p; p || AB, |p,AB|= 2 cm
3) ∢BAX; |∢BAX|= 75°
4) C; C ∈ p ∩ ⟼ AX
5) ∢ABY; |∢ABY|= 30°
6) D; D ∈ p ∩ ⟼ BY
7) lichoběžník ABCD
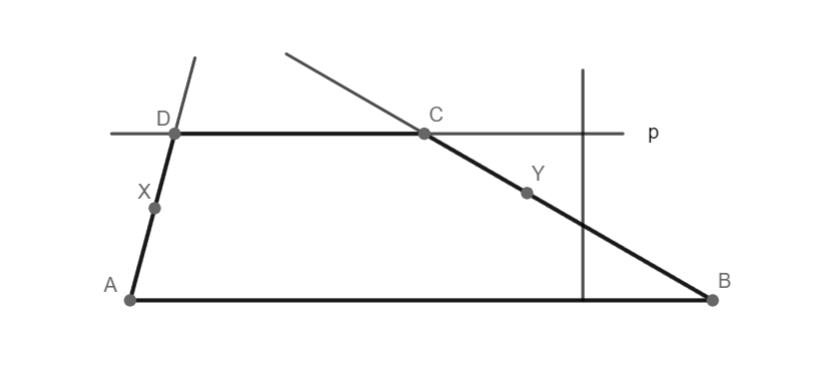
Lichoběžník ABCD souhlasí, 1 řešení.
a = 5 cm; c = 3,5 cm; β = 70°; v = 3 cm
Sestrojte lichoběžník ABCD.
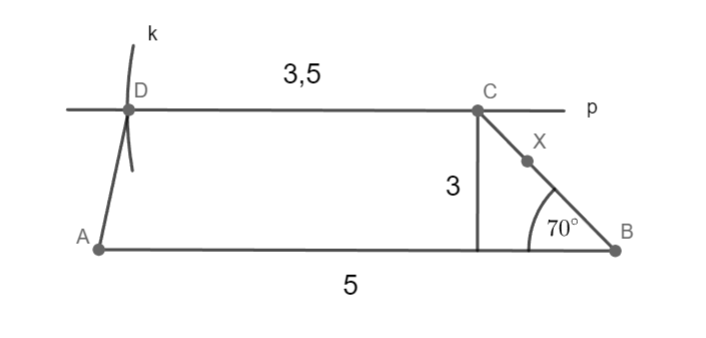
AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ BX
C ∈ p ∩ ⟼ BX
D ∈ p; p || AB
D ∈ k; k(C; 3,5 cm)
D ∈ p ∩ k
1) AB; |AB|= 5 cm
2) p; p || AB, |p,AB|= 3 cm
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ p ∩ ⟼ BX
5) k; k(C; 3,5 cm)
6) D; D ∈ p ∩ k
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
a = 3,7 cm; d = 3 cm; α = 50°; |AC|= 8 cm
Sestrojte lichoběžník ABCD.
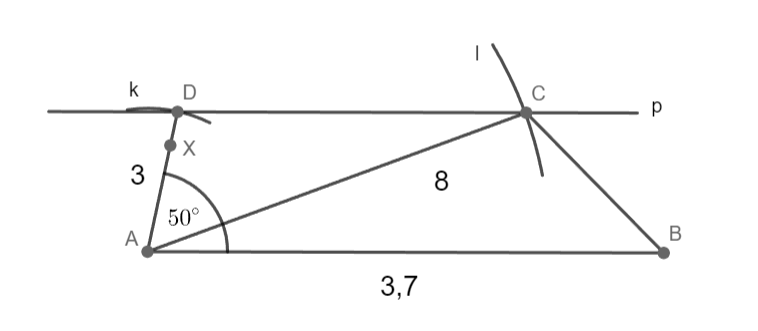
AB
DC
________________
D ∈ ⟼ AX
D ∈ k; k(A; 3 cm)
D ∈ ⟼ AX ∩ k
C ∈ p; p || AB, D ∈ p
C ∈ l; l(A; 8 cm)
C ∈ p ∩ l
1) AB; |AB|= 3,7 cm
2) ∢BAX; |∢BAX|= 50°
3) k; k(A; 3 cm)
4) D; D ∈ k ∩ ⟼ AX
5) p; p || AB, D ∈ p
5) l; l(A; 8 cm)
6) C; C ∈ p ∩ l
7) lichoběžník ABCD
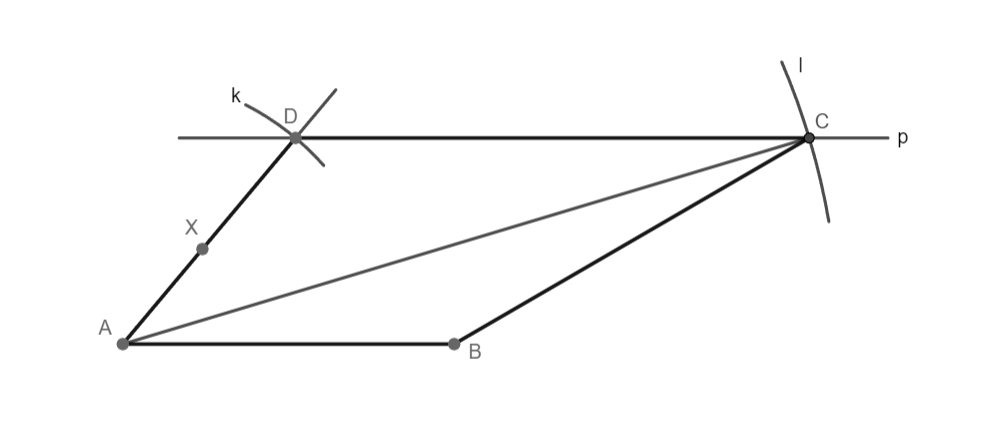
Lichoběžník ABCD souhlasí, 1 řešení.
a = 6 cm; b = 7 cm; c = 9 cm
Sestrojte trojúhelník ABC.

AB
C
_________________
C ∈ k; k(A; 7 cm)
C ∈ l; l(B; 6 cm)
C ∈ k ∩ l
1) AB; |AB|= 9 cm
2) k; k(A; 7 cm)
3) l; l(B; 6 cm)
4) C; C ∈ k ∩ l
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
a = 6 cm; c = 8 cm; β = 55°
Sestrojte trojúhelník ABC.

AB
C
_________________
C ∈ k; k(B; 6 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
1) AB; |AB|= 8 cm
2) k; k(B; 6 cm)
3) ∢ABX; |∢ABX|= 55°
4) C; C ∈ k ∩ ⟼ BX
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
c = 7 cm; α = 40°; β = 35°
Sestrojte trojúhelník ABC.

AB
C
________________
C ∈ ⟼ AX
C ∈ ⟼ BY
C ∈ ⟼ AX ∩ ∈ ⟼ BY
1) AB; |AB|= 7 cm
2) ∢BAX; |∢BAX|= 40°
3) ∢ABY; |∢ABY|= 35°
4) C; C ∈ ⟼ AX ∩ ∈ ⟼ BY
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
k = 8 cm; m = 7,5 cm; |∢KLM|= 80°
Sestrojte trojúhelník KLM.

KL
M
________________
M ∈ k; k(L; 8 cm)
M ∈ ⟼ LX
M ∈ k ∩ ⟼ LX
1) KL; |KL|= 7,5 cm
2) k; k(L; 8 cm)
3) ∢KLX; |∢KLX|= 80°
4) M; M ∈ k ∩ ⟼ LX
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
k = 6 cm; |∢KLM|= 20°; |∢LMK|= 110°
Sestrojte trojúhelník KLM.

LM
K
________________
K ∈ ⟼ LX
K ∈ ⟼ MY
K ∈ ⟼ LX ∩ ∈ ⟼ MY
1) LM; |LM|= 6 cm
2) ∢MLX; |∢MLX|= 20°
3) ∢LMY; |∢LMY|= 110°
4) K; K ∈ ⟼ LX ∩ ∈ ⟼ MY
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
k = 3 cm; l = 4 cm; m = 5 cm
Sestrojte trojúhelník KLM.

KL
M
________________
M ∈ k; k(K; 4 cm)
M ∈ l; l(L; 3 cm)
M ∈ k ∩ l
1) KL; |KL|= 5 cm
2) k; k(K; 4 cm)
3) l; l(L; 3 cm)
4) M; M ∈ k ∩ l
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
o = 7 cm; p = 12 cm; q = 6 cm
Sestrojte trojúhelník OPQ.

OP
Q
________________
Q ∈ k; k(O; 12 cm)
Q ∈ l; l(P; 7 cm)
Q ∈ k ∩ l
1) OP; |OP|= 6 cm
2) k; k(O; 12 cm)
3) l; l(P; 7 cm)
4) Q; Q ∈ k ∩ l
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
p = 5 cm; |∢QOP|= 70°; |∢PQO|= 80°
Sestrojte trojúhelník OPQ.

QO
P
________________
P ∈ ⟼ QX
P ∈ ⟼ OY
P ∈ ⟼ QX ∩ ∈ ⟼ OY
1) QO; |QO|= 5 cm
2) ∢OQX; |∢OQX|= 80°
3) ∢QOY; |∢QOY|= 70°
4) P; P ∈ ⟼ QX ∩ ∈ ⟼ OY
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
o = 4 cm; p = 7 cm; |∢PQO|= 42°
Sestrojte trojúhelník OPQ.

PQ
O
________________
O ∈ k; k(Q; 7 cm)
O ∈ ⟼ QX
O ∈ k ∩ ⟼ QX
1) PQ; |PQ|= 7,5 cm
2) k; k(Q; 7 cm)
3) ∢PQX; |∢PQX|= 42°
4) O ∈ k ∩ ⟼ QX
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
m = 6 cm; n = 3,5 cm; |∢MNO|= 30°
Sestrojte trojúhelník MNO.

NO
M
________________
M ∈ k; k(O; 3,5 cm)
M ∈ ⟼ NX
M ∈ k ∩ ⟼ NX
1) NO; |NO|= 6 cm
2) k; k(O; 3,5 cm)
3) ∢ONX; |∢ONX|= 30°
4) M; M ∈ k ∩ ⟼ NX
5) trojúhelník MNO

Trojúhelník MNO souhlasí, 1 řešení.
e = 6 cm; f = 4,5 cm; |∢GEF|= 90°
Sestrojte trojúhelník EFG.

GE
F
________________
F ∈ k; k(G; 6 cm)
F ∈ ⟼ EX
F ∈ k ∩ ⟼ EX
1) EF; |EF|= 4,5 cm
2) k; k(G; 6 cm)
3) ∢GEX; |∢GEX|= 90°
4) F; F ∈ k ∩ ⟼ EX
5) trojúhelník EFG

Trojúhelník EFG souhlasí, 1 řešení.
s = 10,8 cm; t = 7 cm; |∢RST|= 114°
Sestrojte trojúhelník RST.

RS
T
________________
T ∈ k; k(R; 10,8 cm)
T ∈ ⟼ SX
T ∈ k ∩ ⟼ SX
1) RS; |RS|= 4,5 cm
2) k; k(R; 10,8 cm)
3) ∢RSX; |∢RSX|= 114°
4) T; T ∈ k ∩ ⟼ SX
5) trojúhelník RST

Trojúhelník RST souhlasí, 1 řešení.
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník ABCD.

AB
CD
________________
C ∈ k; k(B; 4 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
D ∈ l; l(C; 3 cm)
D ∈ ⟼ CY
D ∈ l ∩ ⟼ CY
1) AB; |AB|= 7 cm
2) k; k(B; 4 cm)
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ k ∩ ⟼ BX
5) l; l(C; 3 cm)
6) ∢BCY; |∢BCY|= 100°
7) D; D ∈ l ∩ ⟼ CY
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 1 řešení.
a = c = 6 cm; b = d = 2,5 cm; |AC|= 7 cm
Sestrojte čtyřúhelník ABCD.

AB
CD
________________
C ∈ l; l(B; 2,5 cm)
C ∈ m; m(A; 7 cm)
C ∈ l ∩ m
D ∈ k; k(A; 2,5 cm)
D ∈ n; n(C; 6 cm)
D ∈ k ∩ n
1) AB; |AB|= 6 cm
2) l; l(B; 2,5 cm)
3) m; m(A; 7 cm)
4) C; C ∈ l ∩ m
5) k; k(A; 2,5 cm)
6) n; n(C; 6 cm)
7) D; D ∈ k ∩ n
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 1 řešení.
d = 6,5 cm; |AC|= 7,5 cm; |BD|= 5 cm; |∢CAB|= 12°; |∢BAD|= 35°
Sestrojte čtyřúhelník ABCD.

AD
CB
________________
C ∈ ⟼ AX
C ∈ k; k(A; 7,5 cm)
C ∈ ⟼ AX ∩ k
B ∈ ⟼ AY
B ∈ l; l(D; 6 cm)
B ∈ ⟼ AY ∩ l
1) AD; |AD|= 6,5 cm
2) ∢DAX; |∢DAX|= 12°
3) k; k(A; 7,5 cm)
4) C ∈ ⟼ AX ∩ k
5) ∢DAY; |∢DAY|= 35°
6) l; l(D; 6 cm)
7) B ∈ ⟼ AY ∩ l
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 2 řešení.
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník MNOP.

trojúhelník MPO
N
________________
N ∈ ⟼ OZ
N ∈ ⟼ MX
N ∈ ∈ ⟼ OZ ∩ ⟼ MX
1) trojúhelník MPO (SUS)
2) ∢POZ; |∢POZ|= 67°
3) ∢PMX; |∢PMX|= 45°
4) N; N ∈ ⟼ OZ ∩ ⟼ MX
5) čtyřúhelník MNOP

Čtyřúhelník MNOP souhlasí, 1 řešení.
|AC|=|BD|= 4 cm
Sestrojte čtyřúhelník ABCD.

AC
BD
________________
B ∈ ↔ SX; ↔ SX ⊥ AC
B ∈ k; k(S; 2 cm)
B ∈ ↔ SX ∩ k
D ∈ ↔ SX; ↔ SX ⊥ AC
D ∈ l; l(S; 2 cm)
D ∈ ↔ SX ∩ l
1) AC; |AC|= 4 cm
2) S; |SA|=|SC|, S ∈ AC
3) ↔ SX; ↔ SX ⊥ AC
4) k; k(S; 2 cm)
5) B ∈ ↔ SX ∩ k
6) l; l(S; 2 cm)
7) D ∈ ↔ SX ∩ l
8) čtverec ABCD

Čtverec ABCD souhlasí, 1 řešení.
a = 7 cm; α = 75°; β = 30°; v = 2 cm
Sestrojte lichoběžník ABCD.

AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ AX
C ∈ p ∩ ⟼ AX
D ∈ p; p || AB
D ∈ ⟼ BY
D ∈ p ∩ ⟼ BY
1) AB; |AB|= 7 cm
2) p; p || AB, |p,AB|= 2 cm
3) ∢BAX; |∢BAX|= 75°
4) C; C ∈ p ∩ ⟼ AX
5) ∢ABY; |∢ABY|= 30°
6) D; D ∈ p ∩ ⟼ BY
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
a = 5 cm; c = 3,5 cm; β = 70°; v = 3 cm
Sestrojte lichoběžník ABCD.

AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ BX
C ∈ p ∩ ⟼ BX
D ∈ p; p || AB
D ∈ k; k(C; 3,5 cm)
D ∈ p ∩ k
1) AB; |AB|= 5 cm
2) p; p || AB, |p,AB|= 3 cm
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ p ∩ ⟼ BX
5) k; k(C; 3,5 cm)
6) D; D ∈ p ∩ k
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
a = 3,7 cm; d = 3 cm; α = 50°; |AC|= 8 cm
Sestrojte lichoběžník ABCD.

AB
DC
________________
D ∈ ⟼ AX
D ∈ k; k(A; 3 cm)
D ∈ ⟼ AX ∩ k
C ∈ p; p || AB, D ∈ p
C ∈ l; l(A; 8 cm)
C ∈ p ∩ l
1) AB; |AB|= 3,7 cm
2) ∢BAX; |∢BAX|= 50°
3) k; k(A; 3 cm)
4) D; D ∈ k ∩ ⟼ AX
5) p; p || AB, D ∈ p
5) l; l(A; 8 cm)
6) C; C ∈ p ∩ l
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
1) Vyřešte konstrukční úlohy:
a = 6 cm; b = 7 cm; c = 9 cm
Sestrojte trojúhelník ABC
a = 6 cm; b = 7 cm; c = 9 cm
Sestrojte trojúhelník ABC.

AB
C
_________________
C ∈ k; k(A; 7 cm)
C ∈ l; l(B; 6 cm)
C ∈ k ∩ l
1) AB; |AB|= 9 cm
2) k; k(A; 7 cm)
3) l; l(B; 6 cm)
4) C; C ∈ k ∩ l
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
a = 6 cm; c = 8 cm; β = 55°
Sestrojte trojúhelník ABC
a = 6 cm; c = 8 cm; β = 55°
Sestrojte trojúhelník ABC.

AB
C
________________
C ∈ k; k(B; 6 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
1) AB; |AB|= 8 cm
2) k; k(B; 6 cm)
3) ∢ABX; |∢ABX|= 55°
4) C; C ∈ k ∩ ⟼ BX
5) trojúhelník ABC
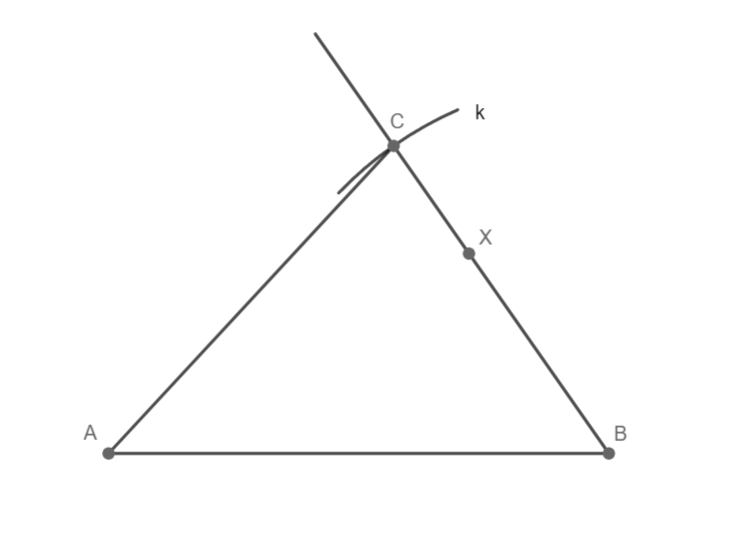
Trojúhelník ABC souhlasí, 1 řešení.
c = 7 cm; α = 40°; β = 35°
Sestrojte trojúhelník ABC
c = 7 cm; α = 40°; β = 35°
Sestrojte trojúhelník ABC.

AB
C
________________
C ∈ ⟼ AX
C ∈ ⟼ BY
C ∈ ⟼ AX ∩ ∈ ⟼ BY
1) AB; |AB|= 7 cm
2) ∢BAX; |∢BAX|= 40°
3) ∢ABY; |∢ABY|= 35°
4) C; C ∈ ⟼ AX ∩ ∈ ⟼ BY
5) trojúhelník ABC

Trojúhelník ABC souhlasí, 1 řešení.
k = 8 cm; m = 7,5 cm; |∢KLM|= 80°
Sestrojte trojúhelník KLM
k = 8 cm; m = 7,5 cm; |∢KLM|= 80°
Sestrojte trojúhelník KLM.

KL
M
________________
M ∈ k; k(L; 8 cm)
M ∈ ⟼ LX
M ∈ k ∩ ⟼ LX
1) KL; |KL|= 7,5 cm
2) k; k(L; 8 cm)
3) ∢KLX; |∢KLX|= 80°
4) M; M ∈ k ∩ ⟼ LX
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
k = 6 cm; |∢KLM|= 20°; |∢LMK|= 110°
Sestrojte trojúhelník KLM
k = 6 cm; |∢KLM|= 20°; |∢LMK|= 110°
Sestrojte trojúhelník KLM.

LM
K
________________
K ∈ ⟼ LX
K ∈ ⟼ MY
K ∈ ⟼ LX ∩ ∈ ⟼ MY
1) LM; |LM|= 6 cm
2) ∢MLX; |∢MLX|= 20°
3) ∢LMY; |∢LMY|= 110°
4) K; K ∈ ⟼ LX ∩ ∈ ⟼ MY
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
k = 3 cm; l = 4 cm; m = 5 cm
Sestrojte trojúhelník KLM
k = 3 cm; l = 4 cm; m = 5 cm
Sestrojte trojúhelník KLM.

KL
M
________________
M ∈ k; k(K; 4 cm)
M ∈ l; l(L; 3 cm)
M ∈ k ∩ l
1) KL; |KL|= 5 cm
2) k; k(K; 4 cm)
3) l; l(L; 3 cm)
4) M; M ∈ k ∩ l
5) trojúhelník KLM

Trojúhelník KLM souhlasí, 1 řešení.
o = 7 cm; p = 12 cm; q = 6 cm
Sestrojte trojúhelník OPQ
o = 7 cm; p = 12 cm; q = 6 cm
Sestrojte trojúhelník OPQ.

OP
Q
________________
Q ∈ k; k(O; 12 cm)
Q ∈ l; l(P; 7 cm)
Q ∈ k ∩ l
1) OP; |OP|= 6 cm
2) k; k(O; 12 cm)
3) l; l(P; 7 cm)
4) Q; Q ∈ k ∩ l
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
p = 5 cm; |∢QOP|= 70°; |∢PQO|= 80°
Sestrojte trojúhelník OPQ
p = 5 cm; |∢QOP|= 70°; |∢PQO|= 80°
Sestrojte trojúhelník OPQ.

QO
P
________________
P ∈ ⟼ QX
P ∈ ⟼ OY
P ∈ ⟼ QX ∩ ∈ ⟼ OY
1) QO; |QO|= 5 cm
2) ∢OQX; |∢OQX|= 80°
3) ∢QOY; |∢QOY|= 70°
4) P; P ∈ ⟼ QX ∩ ∈ ⟼ OY
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
o = 4 cm; p = 7 cm; |∢PQO|= 42°
Sestrojte trojúhelník OPQ
o = 4 cm; p = 7 cm; |∢PQO|= 42°
Sestrojte trojúhelník OPQ.

PQ
O
________________
O ∈ k; k(Q; 7 cm)
O ∈ ⟼ QX
O ∈ k ∩ ⟼ QX
1) PQ; |PQ|= 7,5 cm
2) k; k(Q; 7 cm)
3) ∢PQX; |∢PQX|= 42°
4) O ∈ k ∩ ⟼ QX
5) trojúhelník OPQ

Trojúhelník OPQ souhlasí, 1 řešení.
m = 6 cm; n = 3,5 cm; |∢MNO|= 30°
Sestrojte trojúhelník MNO
m = 6 cm; n = 3,5 cm; |∢MNO|= 30°
Sestrojte trojúhelník MNO.

NO
M
________________
M ∈ k; k(O; 3,5 cm)
M ∈ ⟼ NX
M ∈ k ∩ ⟼ NX
1) NO; |NO|= 6 cm
2) k; k(O; 3,5 cm)
3) ∢ONX; |∢ONX|= 30°
4) M; M ∈ k ∩ ⟼ NX
5) trojúhelník MNO

Trojúhelník MNO souhlasí, 1 řešení.
e = 6 cm; f = 4,5 cm; |∢GEF|= 90°
Sestrojte trojúhelník EFG
e = 6 cm; f = 4,5 cm; |∢GEF|= 90°
Sestrojte trojúhelník EFG.

GE
F
________________
F ∈ k; k(G; 6 cm)
F ∈ ⟼ EX
F ∈ k ∩ ⟼ EX
1) EF; |EF|= 4,5 cm
2) k; k(G; 6 cm)
3) ∢GEX; |∢GEX|= 90°
4) F; F ∈ k ∩ ⟼ EX
5) trojúhelník EFG

Trojúhelník EFG souhlasí, 1 řešení.
s = 10,8 cm; t = 7 cm; |∢RST|= 114°
Sestrojte trojúhelník RST
s = 10,8 cm; t = 7 cm; |∢RST|= 114°
Sestrojte trojúhelník RST.

RS
T
________________
T ∈ k; k(R; 10,8 cm)
T ∈ ⟼ SX
T ∈ k ∩ ⟼ SX
1) RS; |RS|= 4,5 cm
2) k; k(R; 10,8 cm)
3) ∢RSX; |∢RSX|= 114°
4) T; T ∈ k ∩ ⟼ SX
5) trojúhelník RST

Trojúhelník RST souhlasí, 1 řešení.
2) Vyřešte konstrukční úlohy:
a = 7 cm; b = 4 cm; c = 3 cm; β = 70°; γ = 100°
Sestrojte čtyřúhelník ABCD
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník ABCD.

AB
CD
________________
C ∈ k; k(B; 4 cm)
C ∈ ⟼ BX
C ∈ k ∩ ⟼ BX
D ∈ l; l(C; 3 cm)
D ∈ ⟼ CY
D ∈ l ∩ ⟼ CY
1) AB; |AB|= 7 cm
2) k; k(B; 4 cm)
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ k ∩ ⟼ BX
5) l; l(C; 3 cm)
6) ∢BCY; |∢BCY|= 100°
7) D; D ∈ l ∩ ⟼ CY
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 1 řešení.
a = c = 6 cm; b = d = 2,5 cm; |AC|= 7 cm
Sestrojte čtyřúhelník ABCD
a = c = 6 cm; b = d = 2,5 cm; |AC|= 7 cm
Sestrojte čtyřúhelník ABCD.

AB
CD
________________
C ∈ l; l(B; 2,5 cm)
C ∈ m; m(A; 7 cm)
C ∈ l ∩ m
D ∈ k; k(A; 2,5 cm)
D ∈ n; n(C; 6 cm)
D ∈ k ∩ n
1) AB; |AB|= 6 cm
2) l; l(B; 2,5 cm)
3) m; m(A; 7 cm)
4) C; C ∈ l ∩ m
5) k; k(A; 2,5 cm)
6) n; n(C; 6 cm)
7) D; D ∈ k ∩ n
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 1 řešení.
d = 6,5 cm; |AC|= 7,5 cm; |BD|= 5 cm; |∢CAB|= 12°; |∢BAD|= 35°
Sestrojte čtyřúhelník ABCD
d = 6,5 cm; |AC|= 7,5 cm; |BD|= 5 cm; |∢CAB|= 12°; |∢BAD|= 35°
Sestrojte čtyřúhelník ABCD.

AD
CB
________________
C ∈ ⟼ AX
C ∈ k; k(A; 7,5 cm)
C ∈ ⟼ AX ∩ k
B ∈ ⟼ AY
B ∈ l; l(D; 6 cm)
B ∈ ⟼ AY ∩ l
1) AD; |AD|= 6,5 cm
2) ∢DAX; |∢DAX|= 12°
3) k; k(A; 7,5 cm)
4) C ∈ ⟼ AX ∩ k
5) ∢DAY; |∢DAY|= 35°
6) l; l(D; 6 cm)
7) B ∈ ⟼ AY ∩ l
8) čtyřúhelník ABCD

Čtyřúhelník ABCD souhlasí, 2 řešení.
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník MNOP
o = 4 cm; p = 6 cm; |∢NOP|= 67°; |∢OPM|= 100°; |∢PMN|= 45°
Sestrojte čtyřúhelník MNOP.

trojúhelník MPO
N
________________
N ∈ ⟼ OZ
N ∈ ⟼ MX
N ∈ ∈ ⟼ OZ ∩ ⟼ MX
1) trojúhelník MPO (SUS)
2) ∢POZ; |∢POZ|= 67°
3) ∢PMX; |∢PMX|= 45°
4) N; N ∈ ⟼ OZ ∩ ⟼ MX
5) čtyřúhelník MNOP

Čtyřúhelník MNOP souhlasí, 1 řešení.
|AC|=|BD|= 4 cm
Sestrojte čtyřúhelník ABCD
|AC|=|BD|= 4 cm
Sestrojte čtyřúhelník ABCD.

AC
BD
________________
B ∈ ↔ SX; ↔ SX ⊥ AC
B ∈ k; k(S; 2 cm)
B ∈ ↔ SX ∩ k
D ∈ ↔ SX; ↔ SX ⊥ AC
D ∈ l; l(S; 2 cm)
D ∈ ↔ SX ∩ l
1) AC; |AC|= 4 cm
2) S; |SA|=|SC|, S ∈ AC
3) ↔ SX; ↔ SX ⊥ AC
4) k; k(S; 2 cm)
5) B ∈ ↔ SX ∩ k
6) l; l(S; 2 cm)
7) D ∈ ↔ SX ∩ l
8) čtverec ABCD

Čtverec ABCD souhlasí, 1 řešení.
3) Vyřešte konstrukční úlohy:
a = 7 cm; α = 75°; β = 30°; v = 2 cm
Sestrojte lichoběžník ABCD
a = 7 cm; α = 75°; β = 30°; v = 2 cm
Sestrojte lichoběžník ABCD.

AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ AX
C ∈ p ∩ ⟼ AX
D ∈ p; p || AB
D ∈ ⟼ BY
D ∈ p ∩ ⟼ BY
1) AB; |AB|= 7 cm
2) p; p || AB, |p,AB|= 2 cm
3) ∢BAX; |∢BAX|= 75°
4) C; C ∈ p ∩ ⟼ AX
5) ∢ABY; |∢ABY|= 30°
6) D; D ∈ p ∩ ⟼ BY
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
a = 5 cm; c = 3,5 cm; β = 70°; v = 3 cm
Sestrojte lichoběžník ABCD
a = 5 cm; c = 3,5 cm; β = 70°; v = 3 cm
Sestrojte lichoběžník ABCD.

AB
CD
________________
C ∈ p; p || AB
C ∈ ⟼ BX
C ∈ p ∩ ⟼ BX
D ∈ p; p || AB
D ∈ k; k(C; 3,5 cm)
D ∈ p ∩ k
1) AB; |AB|= 5 cm
2) p; p || AB, |p,AB|= 3 cm
3) ∢ABX; |∢ABX|= 70°
4) C; C ∈ p ∩ ⟼ BX
5) k; k(C; 3,5 cm)
6) D; D ∈ p ∩ k
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
a = 3,7 cm; d = 3 cm; α = 50°; |AC|= 8 cm
Sestrojte lichoběžník ABCD
a = 3,7 cm; d = 3 cm; α = 50°; |AC|= 8 cm
Sestrojte lichoběžník ABCD.

AB
DC
________________
D ∈ ⟼ AX
D ∈ k; k(A; 3 cm)
D ∈ ⟼ AX ∩ k
C ∈ p; p || AB, D ∈ p
C ∈ l; l(A; 8 cm)
C ∈ p ∩ l
1) AB; |AB|= 3,7 cm
2) ∢BAX; |∢BAX|= 50°
3) k; k(A; 3 cm)
4) D; D ∈ k ∩ ⟼ AX
5) p; p || AB, D ∈ p
5) l; l(A; 8 cm)
6) C; C ∈ p ∩ l
7) lichoběžník ABCD

Lichoběžník ABCD souhlasí, 1 řešení.
Přečtěte si o tématu dále

Témata k přijímacím zkouškám z matematiky
Přehled nejčastějších typů úloh: počítání se zlomky a vzorci, rovnice, slovní úlohy, geometrie i procenta. Upozorníme na časté chyby a dáme ti tipy, jak se jim vyhnout. Asi první blok, co člověka napadne je klasické počítání ať už například s mocninami, odmocninami nebo velmi často zlomky. V těchto typech příkladů si student sbírá první body, protože tyto úlohy se řadí mezi ty lehčí. Je však důležité, aby uchazeč neudělal zbytečné chyby jako třeba to, že by celý příklad vynásobil společným jmenovatelem (to se dělá totiž až následně u rovnic), dále uvedení výsledku s opačným znamínkem nebo neuvedení výsledného zlomku v základním tvaru, protože i to je bohužel bráno za chybu a pokud je příklad za 2 body, jeden se automaticky strhává.

Jak sestrojit trojúhelník podle zadání
Konstrukce trojúhelníku je častá úloha v geometrii. Vždy musíme dodržet zadané údaje: délky stran nebo velikosti úhlů. Níže najdete všechny základní případy. Jaká budeme mít zadání? Většinou budeme mít čtveřici různých zadání. Můžeme znát ze zadání všechny strany, můžeme znát dvě strany a jeden úhel apod. Z toho tedy budeme mít zadání SSS, SUS, USU, SSU, kde S je strana a U je úhel. Není tedy jedno, kde se nachází úhel nám známý, jelikož u věty SUS víme, že úhel je tam, kde se strany svírají navzájem.

Jak používat kružítko a pravítko efektivně
Kružítko a pravítko jsou základní pomůcky v geometrii. Umožňují nám rýsovat přesné tvary, konstrukce a geometrické úlohy. Správné používání vám ušetří čas a zajistí přesnost. K čemu pravítko a kružítko? Kdo ovládne kružítko a pravítko, ten zvládne většinu základních geometrických úloh. Přesnost a pečlivost jsou v geometrii zásadní a právě tyto dvě pomůcky ti umožní dosáhnout obojího. V článku najdeš jednoduché rady, tipy a triky, jak s nimi pracovat co nejefektivněji.

Jak najít střed kružnice, těžiště nebo ortocentrum
Geometrie je o přesnosti a je třeba pracovat pečlivě a trpělivě, zde se posuneme v tématu dále a ukážeme si další konstrukce, které nás neminou například v přijímacích zkouškách. Pár slov na úvod V geometrii existuje několik speciálních bodů, které mají pro trojúhelník velký význam. Každý z nich se sestrojuje jiným způsobem a slouží k různým účelům. Podívejme se na střed kružnice opsané, střed kružnice vepsané, těžiště a ortocentrum.
