Číselné obory a výrazy
1) Vypočítejte příklady z oborů N (přirozená čísla) a Z (celá čísla):
– 4 ⋅ 5 – [8 ⋅ (- 6 – 36 : (- 12))] =
[128 : (256 : 8)] : [13 + (- 288 : 24)] – 7 ⋅ (121 + 6 ⋅ (- 21)) =
– 8 ⋅ (18 – 72 : 4) : [22 + (- 1024 : 8)] =
– [3 ⋅ (- 2 – 7 ⋅ 2)] – 47 =
25 – {- 3 ⋅ [12 ⋅ 0 – 2 + (3 – 8 ⋅ 4)] – 4 ⋅ 5} =
– 12 + (9 – 13) + 6 – (8 – 11) + (7 – 12) – (- 4 + 9) =
(9 – 11) – {[(- 15 + 7) – 6] – [(21 + 9 – 22) – (- 6 + 13)]} =
[9 – (2 – 4 ⋅ 3)] – 3 ⋅ {- [- (- 3 – 7 ⋅ 4) – 4 + 6]- 9} =
2) Vypočítejte příklady z oboru Q (racionální čísla):
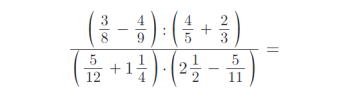
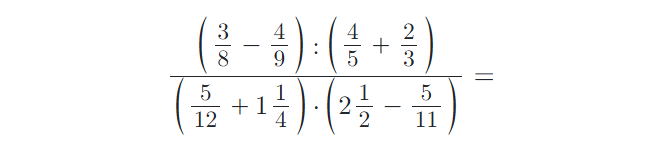
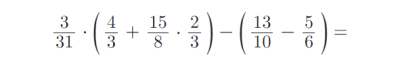
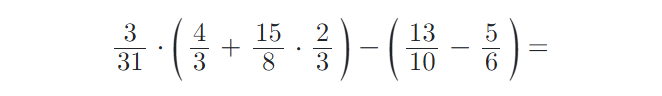
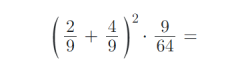
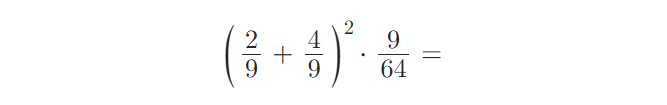
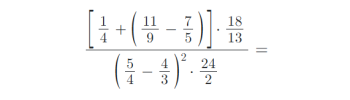
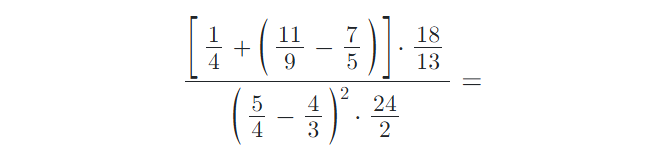
3) Vytvořte ze zadaných zlomků zlomky v základním tvaru:
336 126 =
2408 3010 =
102 1248 =
1242 3726 =
1305 1160 =
686 392 =
4) Vytvořte z periodických čísel zlomky nebo vytvořte ze zlomků periodická čísla:
0,05 =
0,25 =
1,321 =
1,012 =
5,6 =
0,031 =
3 11 =
2122 900 =
451 6 =
3128 176 =
5) Částečně odmocněte:
2√196 =
√99 =
2√175 =
√5040 =
√2156 =
3√490 =
6) Vypočítejte příklady z oboru R (reálných čísel):
√2 ⋅ (4√2 – 3√3) – √3 ⋅ (2√3 – 3√2) =
(5√3 – 3√2)(5√3 + 4√2)
(√2 + √3 – √5)(√2 – √3 + √5) =
(√5 – √7)² =
(- 5√3 + 2√7)² =
(4√7 + 2√6)² =
8√50 + 4√32 – 6√162 =
√98 + √200 + √128 =
7) Usměrněte zlomky tak, aby ve jmenovateli nebyla odmocnina a výsledky uveďte v základním tvaru:
12 √6 =
1 1 + √7 =
15 2√3 - 3 =
4√13 13 - 3√13 =
√3 + √2 √15 + √10 =
5 5 - √5 =
√6 5√7 + 6√3 =
3√5 - 5√3 3√5 + 5√3 =