Rozklad na součin
1) Rozložte na součin vytýkáním:
5x + 10
3y² – 6y
4a³ + 8a²
7x² – 14x + 21
6m³ – 12m² + 18m
9x² – 15x
12a²b – 18ab² + 6b³
40a⁴b⁷ – 60a³b⁹ + 50a⁴b⁵
2) Rozložte na součin podle vzorců:
(x + 5)²
(2y + 3)²
(7 – x)²
(3a + 4b)²
(9x² – 4)
y² – 16
36a² – 49b²
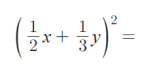
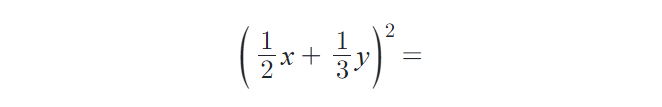
3) Rozložte na součin pomocí postupného vytýkání:
x³ + x² + x + 1
2a³ – 4a² + 3a – 6
4x³ + 6x – 2x² – 3
5x³ + 10x² – x – 2
y³ – y² + 4y – 4
y⁹ – 4y⁷ – 4y⁶ + y⁸
6a² – 9a + 4a – 6
ax + ay + bx + by
4) Rozložte na součin pomocí třetího vzorce:
(x – 3)² – y²
k² + 2kl + l² – m²
m² – 2m + 1 – l² + 2l – 1
a² – 6ab + 9b² – c²
(3x + y)² – z²
(2a + 2b)² – 4c²
5) Rozložte na součin:
5x³ + 10x²
x² + 18x + 81
9x² – 16
3x³ + 2x² + 3x + 2
6a²b – 9ab² + 12ab
4m² + 12m + 9
– 6ay – 6by – 6cy
12x³ – 6x² + 3x
2ax² + 12ax + 18a
70x² + 70y²
Přečtěte si o tématu dále

Témata k přijímacím zkouškám z matematiky
Přehled nejčastějších typů úloh: počítání se zlomky a vzorci, rovnice, slovní úlohy, geometrie i procenta. Upozorníme na časté chyby a dáme ti tipy, jak se jim vyhnout. Asi první blok, co člověka napadne je klasické počítání ať už například s mocninami, odmocninami nebo velmi často zlomky. V těchto typech příkladů si student sbírá první body, protože tyto úlohy se řadí mezi ty lehčí. Je však důležité, aby uchazeč neudělal zbytečné chyby jako třeba to, že by celý příklad vynásobil společným jmenovatelem (to se dělá totiž až následně u rovnic), dále uvedení výsledku s opačným znamínkem nebo neuvedení výsledného zlomku v základním tvaru, protože i to je bohužel bráno za chybu a pokud je příklad za 2 body, jeden se automaticky strhává.

Jak vytknout společný člen
Vytýkání společného členu je jedna z nejzákladnějších algebraických úprav. Používá se k zjednodušení výrazů, k jejich přehlednějšímu zápisu a hlavně jako příprava pro další kroky, například při řešení rovnic, rozkladu na součin nebo práci se vzorci. Co znamená vytknout společný člen Vytknout znamená najít takový faktor, který se vyskytuje ve všech členech výrazu, a tento faktor zapsat před závorku. Výraz v závorce musí být sestaven tak, aby po roznásobení vznikl původní výraz. Výsledkem je kratší a přehlednější tvar, se kterým se lépe pracuje.

Jak použít vzorce pro druhou mocninu
Krácení zlomků je základní dovednost, která vám usnadní celý svět matematiky. Vyzkoušejte si to podle jednoduchých kroků a už nikdy se v tom neztratíte! Jak použít vzorce pro druhou mocninu Vzorce pro druhou mocninu se používají, když chceme rychle roznásobit závorku na druhou nebo naopak rozložit výraz na součin. Jsou to jedny z nejdůležitějších vzorců v algebře, protože výrazně zjednodušují úpravy výrazů i řešení rovnic.

Jak postupně rozkládat složité výrazy
Postupné vytýkání je metoda, kterou použijete tehdy, když nelze vytknout společný člen z celého výrazu najednou. Typicky se s ní setkáte u čtyřčlenů, kde je potřeba výraz rozdělit na části a vytýkat po krocích. Kdy je postupné vytýkání potřeba Tento postup využijete zejména tehdy, když výraz obsahuje více členů, které nemají jeden společný faktor všichni dohromady. Přesto ale v něm lze najít společné části po dvojicích. Postupné vytýkání vám umožní tyto části „odhalit“ a výraz rozložit systematicky.
